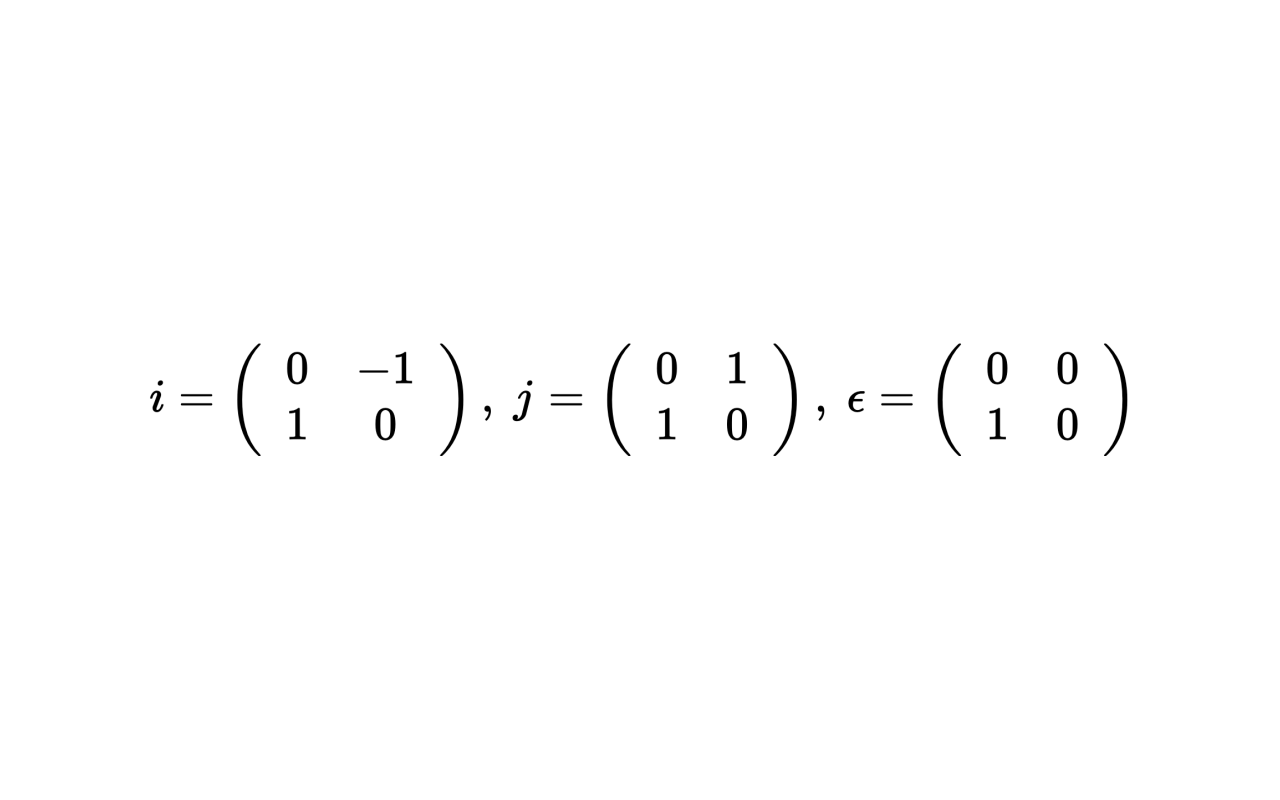コラッツ問題の複素化 (二次元化) で見つけた「似たループ」と「長いループ」
コラッツ問題は「偶数は2で割る、奇数は3倍して1を足す」という操作を繰り返すと、最終的に1に到達するかどうかを問う問題です。
そして、コラッツ予想とは、全ての正の整数についてこの操作を繰り返すと最終的に1に到達する、という予想です。
この予想は未解決問題として有名ですが、私はこのコラッツ問題を「複素数」(ガウス整数)に拡張する方法を考案しました。
この拡張方法については、以前の記事「これも一つのコラッツ問題の複素化」で詳しく説明しています。
ありがとうございましたキミコエドットコム
映画『きみの声をとどけたい』の公式サイトである kimikoe.com ( https://kimikoe.com ) がいつの間にか閉鎖されていました。
当ドメインは、「キミコエ・オーディション」がトップページとして公開されており、 kimikoe.com/movie/ が『きみの声をとどけたい』公式ページの位置付けでした。
映画『きみの声をとどけたい』の情報として、イントロダクションやキャスト(NOW ON AIRの6人に加え、他の重要キャスト)・スタッフ、予告編動画、上映情報、さらに特設の「湘南MAP」などが掲載されていました。
これも一つのコラッツ問題の複素化
本記事は日曜数学アドベントカレンダー2025の5日目の記事です。
私が研究したコラッツ問題の最新の成果です。
コラッツ問題は「与えられた値が偶数ならその値を2で割り、奇数なら3倍して1を足す」という操作を繰り返すと、最終的に1に到達するかどうかを問う問題です。
そして、コラッツ予想とは、全ての正の整数についてこの操作を繰り返すと最終的に1に到達する、という予想です。
例えば、7から始めると以下のようになります。
この予想は未解決問題として有名ですが、私はこのコラッツ問題を「複素数」(ガウス整数)に拡張する方法を考案しました。
私は何よりグラフィカルな表現が好きなので、コラッツ問題の複素化により面白い図形が得られることを期待したのです。
キミコエアドベントカレンダー2025はじまりました
今年もやってきました、キミコエアドベントカレンダー!
今年のアドベントカレンダーはこちら!
キミコエ Advent Calendar 2025 - Adventar
アドベントカレンダー参加者募集!!
アドベントカレンダーは本来は日替わりでブログを書いてカレンダーを埋めるものですが、最近はかなりゆるーく開催しているので、なんとなく「ブログ強化月間」ぐらいに捉えてもらえればと思います。
「アドベントカレンダーって全然わからないんだけど?」という方もコンタクトいただければご案内します。
演算同士の演算
はじめに
集合論において、集合は要素の集まりとして定義されますが、要素が単なる値ではなく、特定の演算を元として持つ場合、その集合の性質や挙動はどのように変わるのでしょうか。例えば、数値の集合に加算や乗算といった演算を元として持たせることが考えられます。
具体的には、次のような場合が考えられます。本記事では基本的に演算同士の2項演算、つまり「演算子と演算子を演算する」ことを考えます。
このように定義すると、2項演算は以下のように書き下せます。
いちおう8通り列挙しましたが、演算子が3つ並んでいるとなんのこっちゃわからないですね。
改めて、演算子の代わりに「Plus」「Times」のような文字列を使って2変数関数として考える(関数として振る舞う、引数を持てる数、と考えてもいいかもしれません)と、次のようになります。
技術2025-08-08: GPT-5が登場したと聞いて
ChatGPTのラインナップにGPT-5が登場したと聞いて、即日で自分なりにまとめつつ、独自のVSCodeへの組み込みをアップデートしました。
いつから?
GPT-5は日本時間では本日発表され、OpenAIからの紹介メールも2025年8月8日 4:18に受信したところです。
何が新しいの?
GPT-5は、即座に回答するGPT-4oなどのモデルと、推論が得意なo3のいいとこ取りをしたモデルのようです。高速モデル(即座)とThinkingモデル(推論)があるとのことですが、それを内部的に切り替えているのでしょうか。
どこで使えるの?
GPT-5は、すでにChatGPTのサービス(無料プランでも!)に組み込まれているようです。なんかカラフルに背景になった!使い方は、ただチャットするだけで、特にモデルを選ぶとかもしなくても、GPT-5が自動的に選ばれるようです。
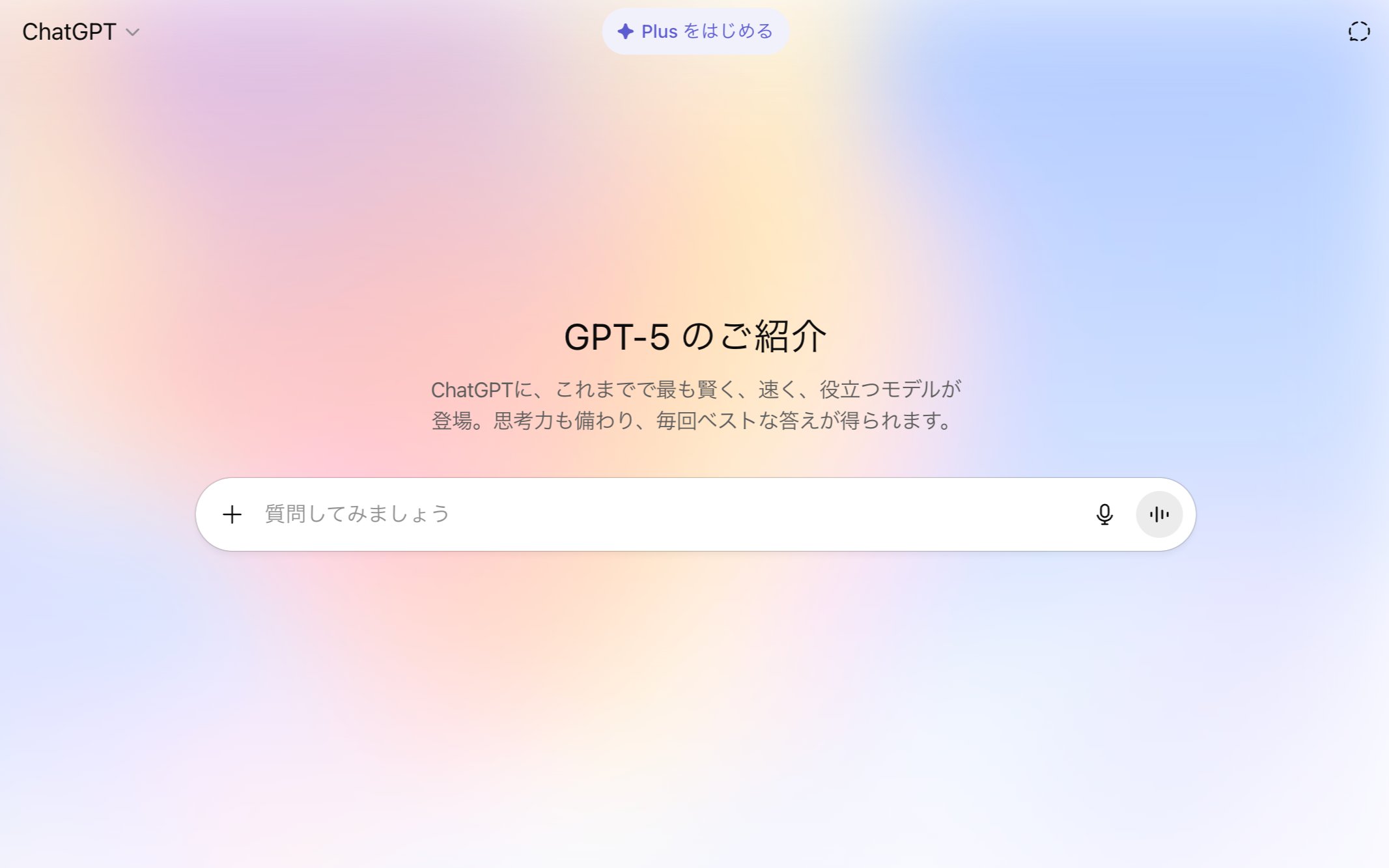
o3が出たときは、o3やo3-miniは無料プランでは限定されていた一方で、GPT-5は無料プランでも発表当日から利用可能なようです(制限はありそう)。 恐らくですが、従来の高性能なモデルに比べて機能向上とリーズナブルな点が合致したのではないでしょうか。
また、OpenAIのAPIを通じても利用可能です。
技術書に書いた技術で技術書の表紙を描いた #技術書典
2025年5月31日より、技術書の同人誌即売会「技術書典」にて、新刊『従量課金で賢く作る!ChatGPT代替AIチャットボット』 (岩淵夕希物智 著、マトラ研究所 発行) が頒布開始されました。
この書籍に詰め込んだ技術で、書籍の表紙も描くことができたので、その際に作ったノートブックを紹介します。
新刊『従量課金で賢く作る!ChatGPT代替AIチャットボット』で賢いAIライフを! #技術書典
2025年5月31日より、技術書の同人誌即売会「技術書典」にて、新刊『従量課金で賢く作る!ChatGPT代替AIチャットボット』 (岩淵夕希物智 著、マトラ研究所 発行) が頒布開始されました。この書籍では、ChatGPTの代替となるAIチャットボットの構築方法を、従量課金制で賢く行うためのノウハウが紹介されています。
「無」を出力するAI
2025年4月20日(日)に、WBAモノづくり発表会というイベントが開催されました。
AIに大いに興味を持つ団体「全脳アーキテクチャ若手の会」の新規イベントで、「普段役に立たないけど,作ってみた!」という作品を披露し、モノづくりの純粋な楽しさを分かち合うイベントとして開催されました。

今回はゲストとして、「無駄づくり」で有名な藤原麻里菜さん、「AIうそにっき」で世間の注目を浴びた鉄塔さんをお招きして、LT発表会のような形式で行われました。
今回私は、「無駄」の「無」の部分と、「無駄づかい」というワードに着目して、 『「無」を出力するAI』と題した発表を行いました。
スライドはこちら。
fucco creative seminar 2025 & 交流会 参加レポート
2025年1月31日、福井市内で行われた「fucco creative seminar 2025 & 交流会」に参加しました。
前回、ふくいクリエイティブホーム「Cream」に登録しましたという記事を書いたのですが、その関連イベントです。
講師の齋藤精一さんらが登壇され、共創から拓かれる地域とビジネスの可能性についてお話しいただきました。
「オロチ数」の発展その2: 「コハク数」
本記事は素数大富豪アドベントカレンダー2024の12日目の記事です。
昨日の記事は二世さんの素数大富豪のルールを多言語化したいでした。素数大富豪は世界で受け入れられるポテンシャルあるから重要!!!
前回はオロチ数と四つ子等を併せた「キュービコリ数」という独自の数を定義し、戦術として使えることを示しました。
今回の重要キーワードはまたしても麻雀用語 (スラング?) の「西ヨーロッパ」です。
「オロチ数」の発展その1: 「キュービコリ数」
本記事は素数大富豪アドベントカレンダー2024の5日目の記事です。
昨日は巨大なナメクジさんの四つ子素数に関する記事でした。じつは本記事も四つ子素数に絡む発展があります。
今回の重要キーワードは麻雀用語の「スジ」です。
日曜数学系イベントの2015年から2024年
この記事は日曜数学 Advent Calendar 2024の4日目の記事です。
2015年が「日曜数学元年」(日曜数学イヤー)ということで、そこから十年の節目だなということでまとめます。
日曜数学会や数学デーなど、趣味で数学活動をしている人たち(日曜数学者)によるイベントを 「日曜数学系イベント」と勝手にカテゴライズしてしまいまして、それらのイベントがどのように盛り上がってきたかをひとつの記事にまとめます。
(なお、2025年には何らかの形でもっと詳細な記事化、あるいは書籍化をしたいと思っています。)
10周年を盛り上げていきたいので、皆さんも活気を持って向き合ってくれると嬉しいです!
桜井政博「ゲーム作るには」のコトダマ
ゲームクリエイターの桜井政博さんがお話していたことがまさに『きみの声をとどけたい』に出てくるコトダマ(言霊)の話だったのでお話しします。
カービィの生みの親
桜井政博さんは「星のカービィ」や「大乱闘スマッシュブラザーズ」などの超有名タイトルを手掛けた超大物ゲームクリエイターです。
…けど、失礼ながらその功績を知ったのはつい最近のことでした。
そんな私はミーハーなのかもしれませんが、桜井さんのYouTube動画シリーズ「ゲーム作るには」の最終回スペシャルを観て大変感銘を受け、もはや私が尊敬するゲームクリエイターの上位に食い込んでくるぐらい興味を惹かれました。
コンピューターゲーム黎明期のレトロゲームを開発していたような方々が、未だ若々しく現役なのって、私たちもかなりレアな世代に生きていると思いませんか?
そんな先駆者の有難いお言葉のひとつが「とにかくやれ!!」です。
キミコエアドベントカレンダー2024はじまりました
今年もやってきました、キミコエアドベントカレンダー!
今年のアドベントカレンダーはこちら!
キミコエ Advent Calendar 2024 - Adventar
アドベントカレンダー参加者募集!!
アドベントカレンダーは本来は日替わりでブログを書いてカレンダーを埋めるものですが、最近はかなりゆるーく開催しているので、なんとなく「ブログ強化月間」ぐらいに捉えてもらえればと思います。
「アドベントカレンダーって全然わからないんだけど?」という方もコンタクトいただければご案内します。
複素整数のわたし的自然な数値フォーマット
プログラミングで複素数を扱おうと思ったら、どう実装しますか?
2024年現在、今でなお複素数をネイティブでサポートしている言語はまだそんなに多くないので、ライブラリを探すか自分で実装するかのどちらかを選択することになるかと思います。
ライブラリとしては、PythonならNumPy、C言語なら<complex.h>、JavaScriptならMath.jsあたりがメジャーそうです。
ライブラリにしろ自分で実装するにしろ、複素数はa + b iのかたちで表せるので「実部と虚部をそれぞれ変数に格納する」が十中八九のソリューションじゃないでしょうか。
否、複素数全体ではなく複素整数(ガウス整数)ですが、実部と虚部をあわせてひとつの整数として扱ってしまったほうが、原理的には計算上簡単になる、という魔法のような数値フォーマットを発明したのでご紹介します。
コラッツの最初の難関
コラッツの問題は定義はとても簡単、でも問題としてはかなりの難問で未解決、という稀有な問題です。
奇数なら3倍して1を足す、偶数なら2で割る、それだけの話。
たとえば3という数は奇数なので3倍して1を足したら10、10は偶数なので2で割って5、5は奇数なので3倍して1を足したら16、16は偶数なので2で割って8、そこから4→2→1と半分にして、そこからは1→4→2→1→4→2...とループになります。
十いくつぐらいでスタートするなら手計算で楽しく計算できますが、27はかなり手強いです。
で、27以降もさらなる強敵がいて、そんな強敵も計算し尽くしてどんな数でも1→4→2のループに落とし込める(1に到達する)という予想が コラッツ予想 です。
いま解ければ1億2000万円の懸賞金がもらえます!
エセJSON
きょうはMachine Learning 15minutes!というイベント(ハイブリッド開催)にかなり久々に参加しました。
いろいろ刺激を受けた中、発表のひとつに「自然言語プログラミング」を試みる話があって、私が2017年から掲げていたオリジナル言語「ce-il」の思想に近いなと感じておりました。
私は今でも言語の研究開発を行っており、改めて「自然言語プログラミング」をどこまでできるか再確認したところ、ChatGPTのちょっと面白い使い方を編み出すことができました(元のアイデアは1年前の2023年4月11日に実験済)。
XMLと比べて可読性が高いといわれるJSONを、あくまでも「人が読むための文章」として使う手法です。
ちょうどWikipediaを開いたら「ラッパスイセン」の項目があったのでこちらの説明文を例として使いました。
新譜『Forte fold』リリースしました
2024年4月28日に行われる #M3春 に先駆けて、Webイベントスペースにてサークル参加しております。
サークル名: 岩淵夕希物智
ジャンル: [A03]音楽一般:テクノ・クラブ
Webイベントスペース: 橙-004
キミコエを全フレーム学習したAIアートの習作
最初に念のため意思表明をしておきます。
AI画像生成については、私自身は肯定的に捉えています。
しかし、世間の声としては主に「イラストレーターや写真家が学習を許可していない画像を勝手に利用されているのは望ましくない」というような理由で忌避されている傾向にあるため、学習及び生成が公開するに相応しいものであるかかなり慎重に判断して掲載しております。
特に今回の実験は特に著作物との類似性が高いものを取り扱っているため、権利者様からの指摘があれば即座に対応します。
前置きはこれぐらいにして、今回の肝は「キミコエをまるっと全フレーム学習して、AIアートへの応用を試みる」というものです。
前回は、既存モデルを利用して、キミコエキャラの特徴からイラストを生成することを試みました。
機械任せでキミコエのファンアートを描いてみる ~Stable Diffusion, NovelAI~
2022年11月26日に行われたサイエンスカフェ(オンライン) 機械任せで絵師になる方法 ~Stable Diffusion, NovelAI~ のレポート記事を兼ねます。
スライドはこちら。
まえがき
自己紹介としては、私は 言語 の創造に携わる博士(工学)で、
中学校と大学で 美術部 に所属していました。
上京して約8年間 Webエンジニア として働いて、その後なんやかんや(入院とか)あって現在に至ります。
美術部に所属していたのもありデッサン力はあるはず(自称)ですし、
大学でも画像や音楽にかかわる研究をしていて芸術に関する素養はあるはず(自称)、
そして仕事もプログラミングがメインながらアニメーションやデザインもそこそこ自力で組めないといけない業務内容だったので芸術センスもあるはず(自称)です。
キミコエアドベントカレンダー2021はじまりました
この記事はキミコエ Advent Calendar 2021 - Adventarの1日目の記事です。
今年もいちおうコトダマ部の企画なのですが、ちょうど11月末(昨日)ブログを改修してうまくいったので発起人・岩淵夕希物智の個人アカウントからの発信としてみました。
アドベントカレンダー参加者募集!!
一時は「アドベントカレンダーを全部埋めよう!」と躍起になってコンプ達成した年もあったのですが、 現在はアドベントカレンダー参加者はゆるーく募集しています。
「アドベントカレンダーってなんじゃ?」という方もコンタクトいただければご案内します。
キミコエが好きすぎて聖地移住して3年目になりました
この記事はキミコエ Advent Calendar 2020の22日目の記事です。
はじめに
2017年8月に公開された映画『きみの声をとどけたい』(以下「キミコエ」)が好きすぎて、舞台である腰越(湘南・鎌倉)に引っ越して3年目になりました。「キミコエ×腰越」のコラボカクテル企画を中心に、今年になってからの新しい変化について書きます。
ラジモ!がくれた松本の思い出
この記事はNOW ON AIR Advent Calendar 2020の16日目の記事です。
今年はもうすっかりリアルイベントが皆無レベルの年で、NOW ON AIRも長らくオンラインでしか会えませんでしたが、それも重なってかなり大きな思い出となる出来事があったので、今日はそれについて語ります。
ちなみに本記事はラジモ 松本 みさみさ にフォーカスを当てていますが、出来事を全体的に綴った記事をすでに公開しているので、こちらもぜひ合わせてお読みください。
素数大富豪プレイヤーが麻雀を打って勝ち得た人生の戦術
この記事は素数大富豪 Advent Calendar 2020の13日目の記事です。
昨日は3TKさんの1年間でどのくらい素数を覚えられるのかの記事でした。
今年も12月13日(QK)の日がやってきました。
1213よりも、13と深い縁があるため素数大富豪研究会の会員番号でもあるこの日を譲れませんでした。
今年のアドベントカレンダーは、マスプライム杯予選が終わったタイミングでは素数大富豪の練習システムを完成させて解説記事を書く決意を持っていましたが、かなり根本的なところにどっぷり踏み込んでしまったためにサグラダファミリアを建てるような途方もなさになってしまい、また別のことを考えることにしました。
白銀輝夜の不思議旅
本記事は、2017年に『きみの声をとどけたい』で不思議体験をした岩淵夕希(物智)が、2020年に今度は『かぐや様は告らせたい』で不思議体験をした出来事を綴ったものです。
お話のはじまり 〜キミコエ、そしてアニメに魂を捧げた者〜
昨年公開した「キミコエが好きすぎて聖地移住して1年経った話」で触れている通り、私は映画『きみの声をとどけたい』(キミコエ)が好きすぎるアニメ好きとして活動しています。
キミコエが好きすぎて聖地移住して1年経った話
この記事はキミコエ Advent Calendar 2019の22日目の記事です。
はじめに
2017年8月に公開された映画『きみの声をとどけたい』(以下「キミコエ」)が好きすぎて、舞台である腰越(湘南・鎌倉)に引っ越して丸1年が経ったところなので、住み始めてからこれまでのことについて語ります。
ペアが重要!素数大富豪の新戦略「魔神出し」
この記事は素数大富豪 Advent Calendar 2019の 13 日目の記事です。
昨日は 3TK さんによる素数大富豪・5 枚出しの鍛え方(自己流)の記事でした。5 枚出しもできるようになりたいものです。
Gitで重いリポジトリをcloneするとき
WordPressの中規模サイトをGitで管理していて、 ファイル容量を圧迫していたので一旦削除したのですが、 今回また修正の必要が出てきてSourceTreeでクローンしようとしたら、
git -c diff.mnemonicprefix=false -c core.quotepath=false -c credential.helper=sourcetree fetch origin
remote: warning: suboptimal pack - out of memory
error: pack-objects died of signal 9
error: git upload-pack: git-pack-objects died with error.
fatal: git upload-pack: aborting due to possible repository corruption on the remote side.
remote: aborting due to possible repository corruption on the remote side.
fatal: protocol error: bad pack header
Completed with errors, see above
と行き詰まってしまいました。
こんなときは多分SourceTreeではどうにもならず、
伝える系の英語とnote, notice, notification…の使い分け
はじめに
「コメントを書く」「言及を行う」「情報を述べる」「説明を書く」あたりの英語(主に名詞)が混同するので、まとめました。
特に、
<div class="note"></div>
<div class="notice"></div>
<div class="notification"></div>
あたりはいつも悩むので、note系とそれ以外でまとめました。
これ系の命名ガイドラインみたいなのがあるかもしれませんが、 使用頻度、結論は筆者のセンスによる独断なので、 「これもよく使う」「いや、こういう用途でははこの命名が鉄板」、とかがあれば教えてください。