研究2025-03-15: フラクタル・ペアの稠密性

投稿日: March 15, 2025

研究

数学

フラクタル

研究2025-03-15: フラクタル・ペアの稠密性

前回のブログ記事で、「新しいフラクタル図形」として「ペンタフレーク・ペア」を紹介しました。

改めて「シェルピンスキーのテーブルクロス」と命名されたフラクタル図形について考え、「ペンタフレーク・ペア」がどういった図形なのかを紐解いてみましょう。

シェルピンスキーのテーブルクロス

大学院生時代に考えていた シェルピンスキーのカーペットの「抜けたところをネガで埋める」という図形 、2011年ごろに研究室Wikiに特性を書いたものの、ログが見つからず記憶の中にしかありませんでした。

しかし、同様の図形はGoogle検索ではいくつか見つかり、まさに全く同じ図形についての記述を見つけました。

シェルピンスキーのテーブルクロス

この図形について、リンクにあるMathematics Stack Exchange上でLarsH氏がこの図形を「シェルピンスキーのテーブルクロス」 (Sierpinski tablecloth) と命名し、以下のように説明しています。

(翻訳)
シェルピンスキー・カーペットの構築は、正方形から始まります。正方形は、3 x 3 のグリッドで 9 つの合同なサブ正方形に切り分けられ、中央の開いたサブ正方形が削除されます。同じ手順が、残りの 8 つのサブ正方形に再帰的に適用され、無限に続きます。
このバリエーションでは、中央のサブスクエアを単に削除するのではなく、同じ手順を「反転で」再帰的に適用します。 (これより適切な言い方がありますか？) つまり、中央の穴を、シェルピンスキー・カーペットの このバリエーションの 補数で置き換えるかのように扱います。
したがって、中央の穴を再帰させるときは、その中央に「反転した穴」（ドーナツのない「ドーナツ穴」のようなもの）を配置します。次に、通常の（正の）手順を使用して反穴を再帰させ、逆の手順を使用して反穴を囲む 8 つのサブスクエアを再帰させます。

この図形について言えることは

積集合は空 (反転であるため)
和集合は正方形 (ハウスドルフ次元が 2)
ポジもネガもハウスドルフ次元は 2 (平面図形)
ポジもネガもどちらも正方形上において稠密
点の個数の比は 1 (1:1) に収束

ということです。

シェルピンスキーのテーブルクロスのイテレーション

図形のピクセル数（正方形の数）が $3^{n} \times 3^{n}$ であるとき、ポジのピクセル数 $s_{n}$ 、ネガのピクセル数 $t_{n}$ 、和のピクセル数 $u_{n}$ は以下のようになります。

n s_{n} t_{n} u_{n} 001111892166581319353672942080448165615211213792859049620689632454553144171979713280325647829698186409602440576143046721

s_{n} t_{n} u_{n} = \frac{9 ^{n} - 7 ^{n}}{2} = \frac{9 ^{n} + 7 ^{n}}{2} = 9^{n}

n \to \infty lim \frac{s _{n}}{t _{n}} = n \to \infty lim \frac{9 ^{n} - 7 ^{n}}{9 ^{n} + 7 ^{n}} = 1

「稠密」はちょっと難しい数学用語ですが、簡単に言うと「ぎっしり詰まっている」、言い換えると「隙間はあっても隙間自体の幅はゼロ」ということです。例として挙げると、実数区間の上では有理数の集合は稠密です。

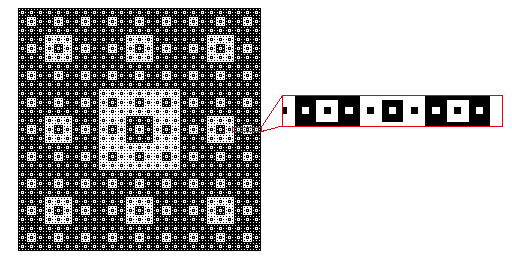
シェルピンスキーのテーブルクロスの中央ライン

シェルピンスキーのテーブルクロスの中央ラインをピックアップすると、黒と白が交互になっていることがわかります。

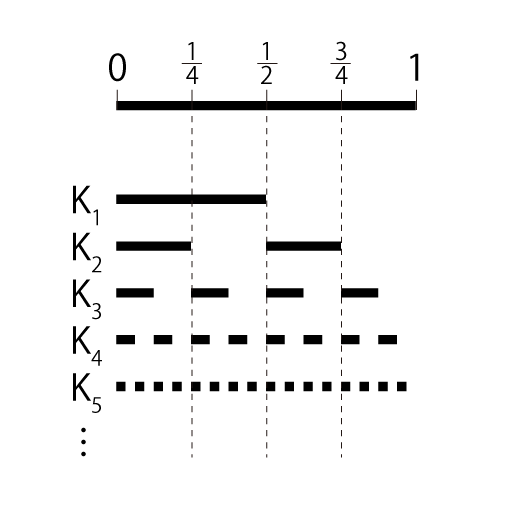
01区間のイテレーション

もっとシンプルな問題に置き換えると、 $[0, 1]$ 区間上で等間隔に交互な線分を引いた時の極限が、どのような1次元図形になるかという問題です。

Stack Exchangeの質問のP.S.にあった互いに密(Interleaving Ad Infinitum)という状態と思われます。

ちょっと不思議なこととしては、1×1の正方形から始めた場合はポジとネガはどちらも1×1の正方形に収束するはずなのに、面積は1/2になるということです。おそらく面積の求め方は測度によって異なるということかもしれませんが、現時点では理解に至っていません。極限値となる図形も、完全に「正方形」と言っていいのか「正方形上の稠密な点集合」としか言えないのか、これもまた疑問です。

ペンタフレーク・ペア再考察

ペンタフレーク・ペアで言えることは

積集合は空 (反転であるため)
和集合はペンタフレーク (ハウスドルフ次元が約1.86)
ポジもネガもハウスドルフ次元は約1.86 (フラクタル図形)
ポジもネガもどちらもペンタフレーク上において稠密
点の個数の比は 1 (1:1) に収束

ということです。

前回の記事では、「新しいフラクタル図形ができたか」ということでした。たしかにイテレーション途中では異なる図形ができているように見えますが、最終的にはペンタフレークに収束していることがわかります。

シェルピンスキーのテーブルクロスのときの四角形を五角形に置き換えると、ポジの5角形の数 $s_{n}$ 、ネガの5角形の数 $t_{n}$ 、和の5角形の数 $u_{n}$ は以下のようになります。

n s_{n} t_{n} u_{n} 0011115621026363761402164520776129653376440077766212802537646656713177614816027993688070408725761679616

s_{n} t_{n} u_{n} = \frac{6 ^{n} - 4 ^{n}}{2} = \frac{6 ^{n} + 4 ^{n}}{2} = 6^{n}

n \to \infty lim \frac{s _{n}}{t _{n}} = n \to \infty lim \frac{6 ^{n} - 4 ^{n}}{6 ^{n} + 4 ^{n}} = 1

基本的な考え方はシェルピンスキーのテーブルクロスと同じですが、大きく異なるのは、収束する図形が正方形（2次元図形）ではなくフラクタル図形（非整数次元の図形）になるということです。

シェルピンスキーのテーブルクロスは遠目に見たら独特の模様が見えますが、ペンタフレーク・ペアは「ちょっと薄いペンタフレーク」に見えるので、やはり直感としては面積が半分になるように見えます。

まとめ

シェルピンスキーのテーブルクロスやシェルピンスキー・ペアの生成法はフラクタル図形として新しい図形を生み出せるわけではないことがはっきりしましたが、シェルピンスキー・ペアの新規性としては、フラクタル図形上の互いに密な点集合を示せたという点にあります。

フラクタル図形自体、非整数次元の図形であるというような「病的な」性質を持っていますが、今回取り上げたようなフラクタル・ペアのまた異なる「病的な」性質をまた深めるとまた面白いかもしれません。