研究2024-06-07: 虚数を「i進数」と考える

かなり前から、「純粋な記数法とは何か」をずっと考えています。

純粋というのは、置換ルールだけを定めるとそこからどんな数システムが生まれるかということです。

実際にこれまで、2進数を拡張して、黄金進数や物智数などといった変わった記数法を考えてきました。

今回はそこで「(i^2 = -1なる) i進数」でもいいよね、という話をより進めて、「(q^4 = 1なる) q進数」でもいいよね、という研究日誌を綴ります。

虚数の簡単な定義

虚数が生まれた経緯は置いておいて、虚数単位iが満たす性質はこうです。

これは言い換えると、二次方程式

の解とも言えます。

もっと言うと、因数分解して

になるのでこの二次方程式の解は ということになります。

i進数という考え方

iは4乗すると1になるので、2進数で2を4乗すると16になるノリで、

と考えてもよさそうです。

iを2乗すると-1 ( を と記します) になる性質も取り入れると、

となり、たとえば

となります。一般化して

となり、2桁に還元できるので、複素数は二元数となるのです。

係数の絶対値が1より小さい(1, -1, 0 で構成される)複素数をi倍 ( 倍) すると以下の離散グラフのような遷移をします。

i倍は複素数平面上の回転を意味するので、i倍を4回繰り返すと元に戻ります。

実際は複素数は任意の実数係数を持つのであくまでも複素数のほんの一部です。

これをi進表記するとこうなります。

4乗すると1になる数の数システム

ここまではただ単に複素数をi進数と言い換えたに過ぎません。

今度は以下の方程式について考えます。

移項して因数分解するとこうなります。

3つの因数のうち最後の因数だけ取り出せば、複素数の定義どおり が得られるのですが、今回の4次方程式の解を俯瞰してみると、「1を引いても0」「1を足しても0」の性質も含んでいてほしい、つまり、 1, -1, i, -i の4つの解の性質をどれも含んでいてほしい、ということになります。

そうすると、先ほどのような といった置換ルールは適用外になります。

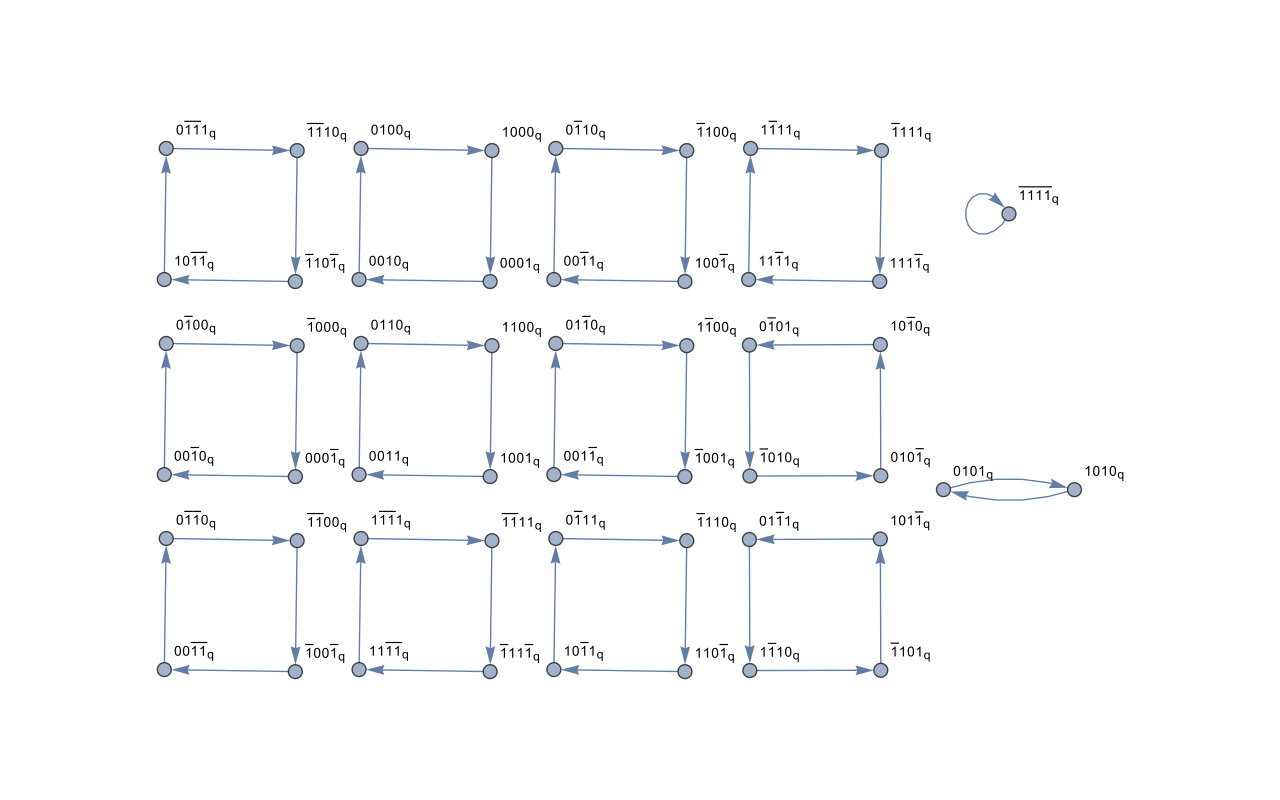
となるi進数に対して となるq進数としておいて、

となります。

そうすると なる数システム上での数は四元数 (一般的な「クォータニオン」とは異なる) になり、この四元数の性質について研究中です。

先ほどと同じように、係数の絶対値が1以下の元をq倍 ( 倍) すると以下のような離散グラフになります。

特筆すべき因数分解

以下の乗算による等式を例示します。

これをそのままq進四元数に適用すると

となります。

同時に、これを2進数として当てはめます。

計算すると

となります。

これを と の2つの多項式が両方3のような性質をもっている数と捉え、9のような性質をもつ数に合成されたと考えます。

また、以下の乗算による等式はどうでしょう。

q進四元数では は元の一つですが、2進数的な見方だと となるので3と5は零因子と言えます。

また、定義からすると自明ではありますが、q進四元数でも の3つの零因子を乗算して0になります。

とりあえずこんなところまででしょうか。