第30回日曜数学会「数表現の万能ブロック」

2024年6月29日の第30回日曜数学会で「数表現の万能ブロック」という発表をしました。

計算機で厳密値を表現する方法として、数値をなんらかの並べ方で組み合わせて表現することができますが、組み合わせ方に自由度が多すぎて扱いづらかったりします。 今回私は、加算、乗算、冪乗の組み合わせによる4引数関数を1ブロックとしてブロックを組み合わせることにより、代数的数の範囲で数の厳密値表現ができる方法を発明しました。 今回の発表では、具体的にどのようなブロックで数が表現できるかご紹介します。

プレゼン動画はこちらです（埋め込み動画はシーク済み）。

資料ページはこちらです。

https://speakerdeck.com/butchi/sunday-math-party-30-notation-block-multi

以下、発表内容をブログ投稿として展開します。

自己紹介

私は言語・記数法の研究者で、物智数の考案者でもあります。今回の「万能ブロック」は記数法研究の派生で生まれたものです。 また、Wolfram言語 (数式処理ソフトMathematicaで扱う言語) のエヴァンジェリストでもあり、Wolfram言語での数表現からインスピレーションを受けています。

計算機で厳密値を表現するには？

Wolfram言語の場合、たとえば を以下のようにFullForm関数で「完全形」を出力します。

1 + Sqrt[2] // FullForm

Times[Rational[1, 2], Plus[1, Power[2, Rational[1, 2]]]]

(これが の厳密値表現)

関数をひとつに

ご覧のように、厳密値表現ではPlus, Times, Powerなど関数をいくつか用意しなければならないので、 ひとつの関数（ブロック）でなんとかならないか？というモチベーションで研究を進めました。

ブロックの定義

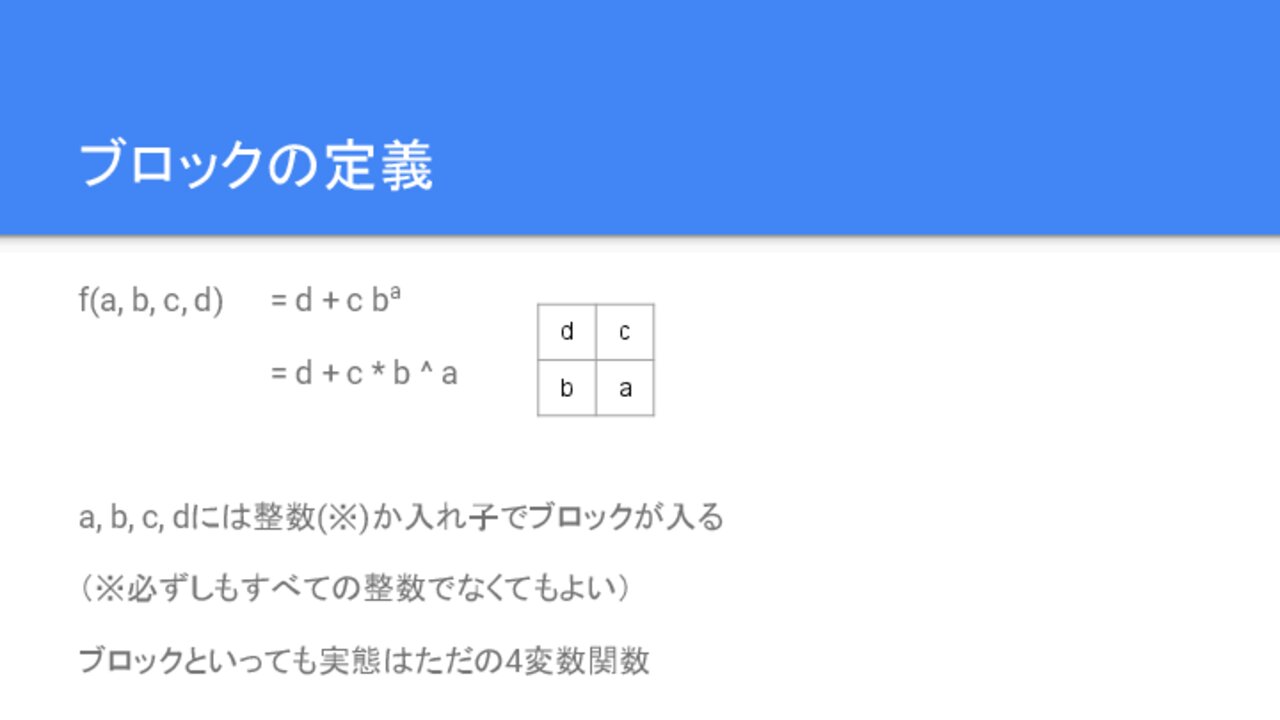
4変数関数fを以下のように定義します。

f(a, b, c, d) = d + c * b ^ a

a, b, c, dには整数 (必ずしもすべての整数でなくてもよい) か入れ子でブロックが入ります。

ブロックといっても実態はただの4変数関数なのですが、2×2の格子状に配列することによって入れ子の可視化がいい具合になります。

整数: 2をつくる

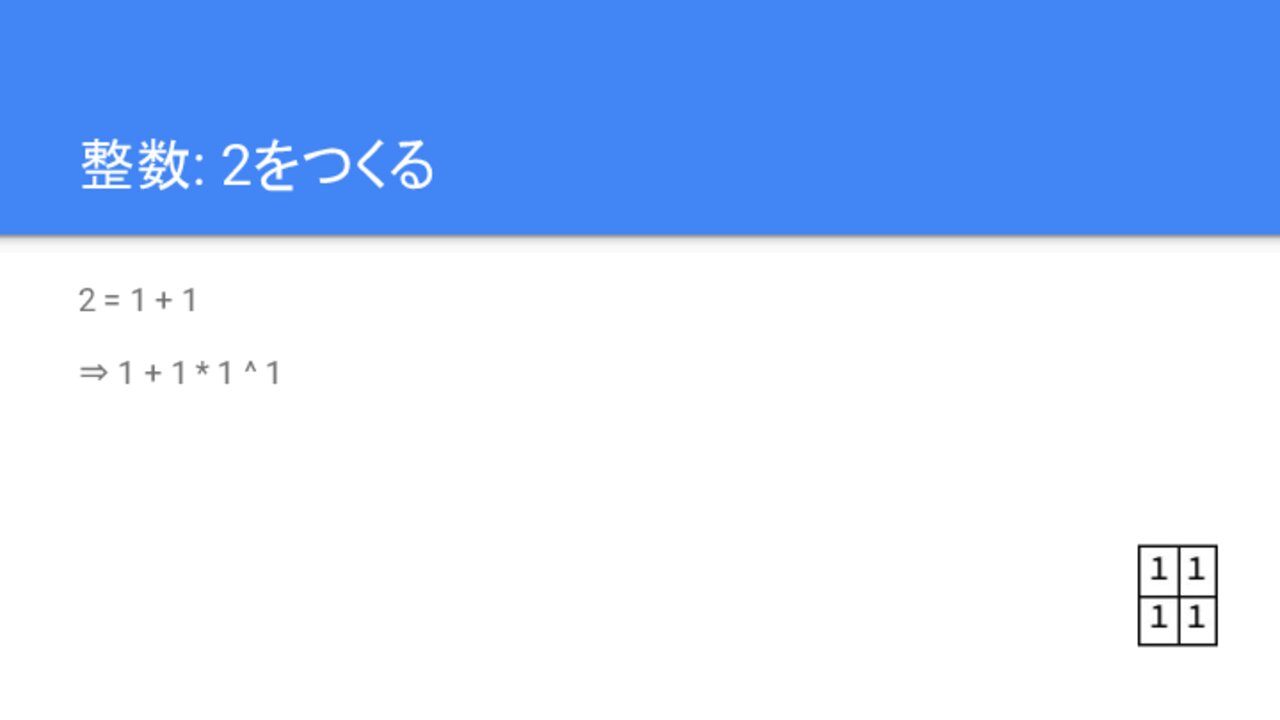
2 = 1 + 1
⇒ 1 + 1 * 1 ^ 1

2は単に「2」として表現してもいいのですが、1だけのブロックから作り出すことができます。

有理数: 1/2をつくる

1/2 = 2 ^ -1
⇒ 0 + 1 * 2 ^ -1

逆数は-1乗なので、冪乗の位置に-1を入れます。

代数的数: √2 をつくる

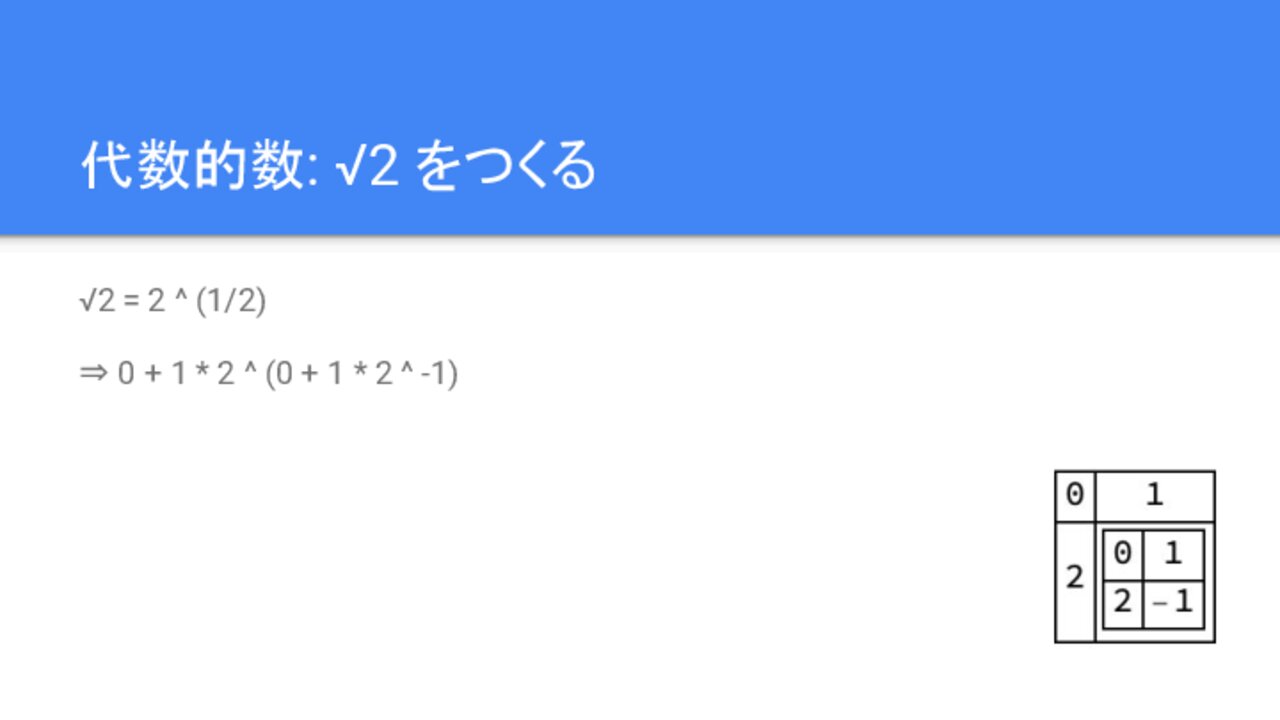
√2 = 2 ^ (1/2)
⇒ 0 + 1 * 2 ^ (0 + 1 * 2 ^ -1)

平方根は1/2乗 (n乗根は1/n乗) なので、冪乗の位置に1/2 (1/n)を入れます。

代数的数: 黄金比をつくる

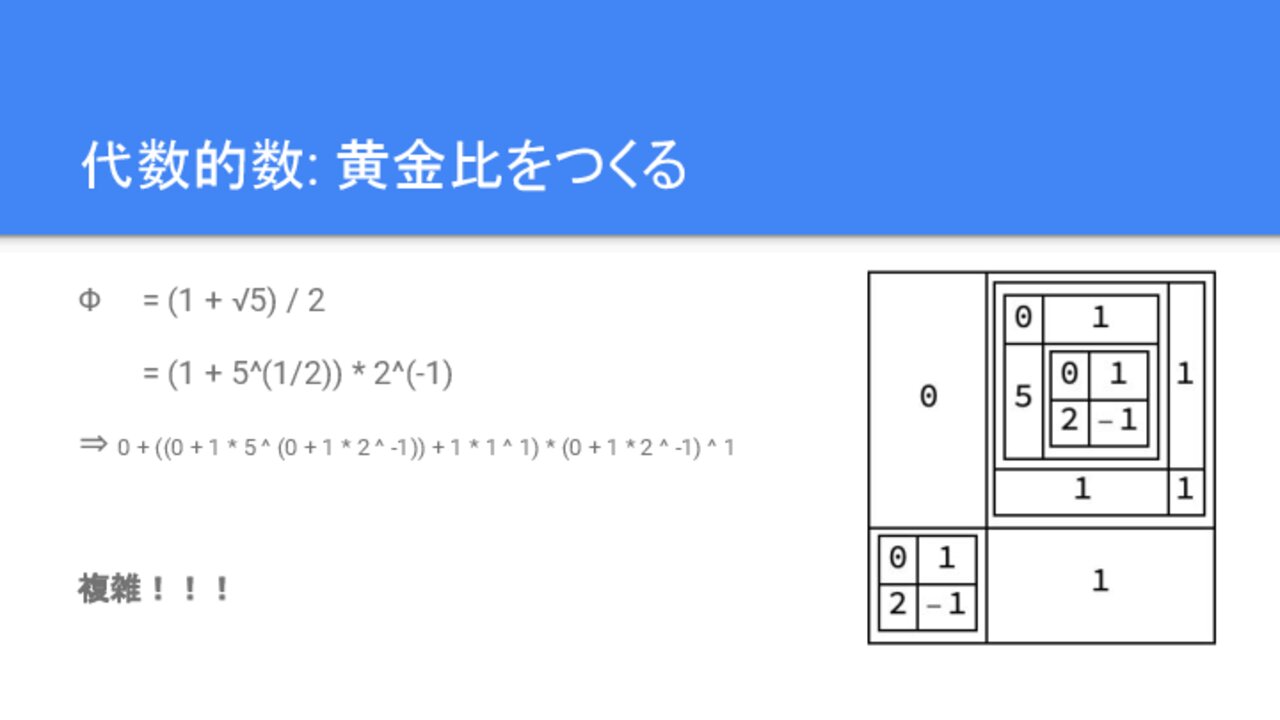
(1 + √5) / 2
= (1 + 5^(1/2)) * 2^(-1)
⇒ 0 + ((0 + 1 * 5 ^ (0 + 1 * 2 ^ -1)) + 1 * 1 ^ 1) * (0 + 1 * 2 ^ -1) ^ 1

入れ子が多いので、パッと見かなり複雑ですね。初見ではすぐに読めないのではないかと思います。

頑張って読んでみる

(1 + √5) / 2
= (1 + 5 ^ (2 ^ -1)) * 2 ^ -1

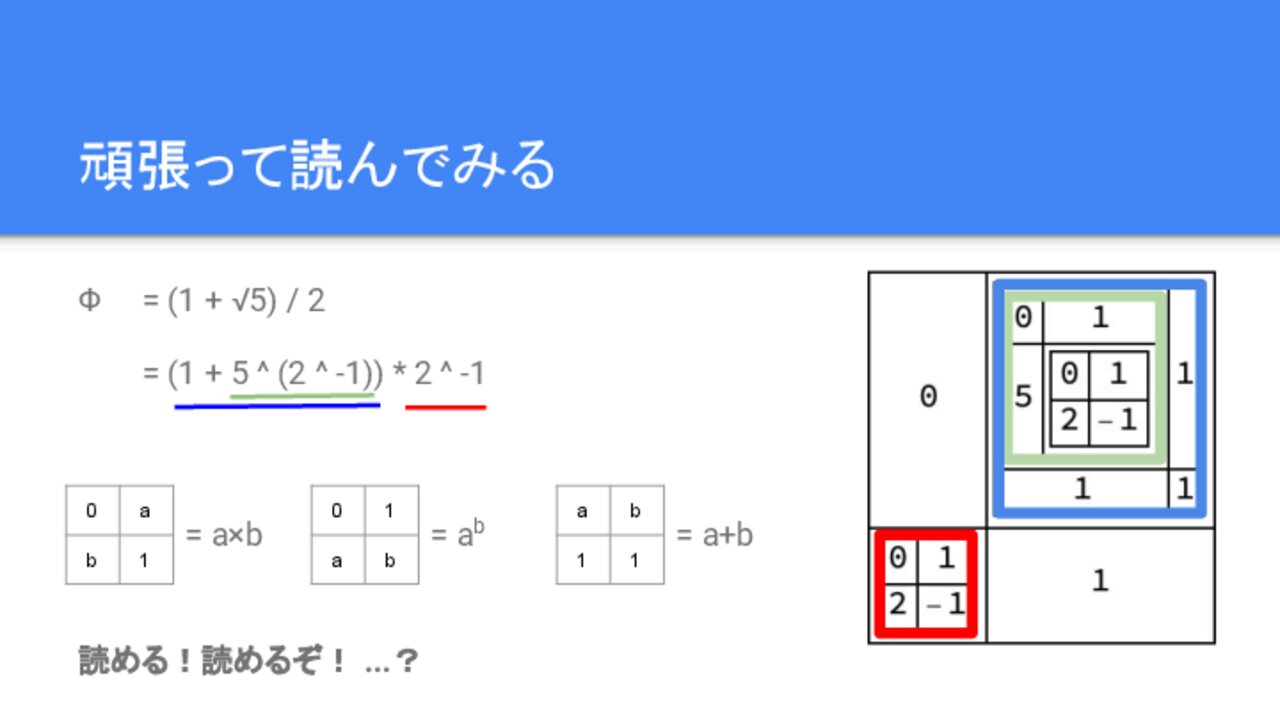
基本的には加算と乗算と冪乗の組み合わせなので、全体を見つつパーツから組み合わせごとに見ていくようにして読んでいけば、慣れで割とスムーズに読めるようになると思います。

原始的な関数

plus(x, y) = x + y * 1 ^ 1  or  x + 1 * y ^ 1
times(x, y) = 0 + x * y ^ 1
power(x, y) = 0 + 1 * x ^ y

これらを使って、減算や除算も含めて四則演算はなんでもできます。

iが使えれば

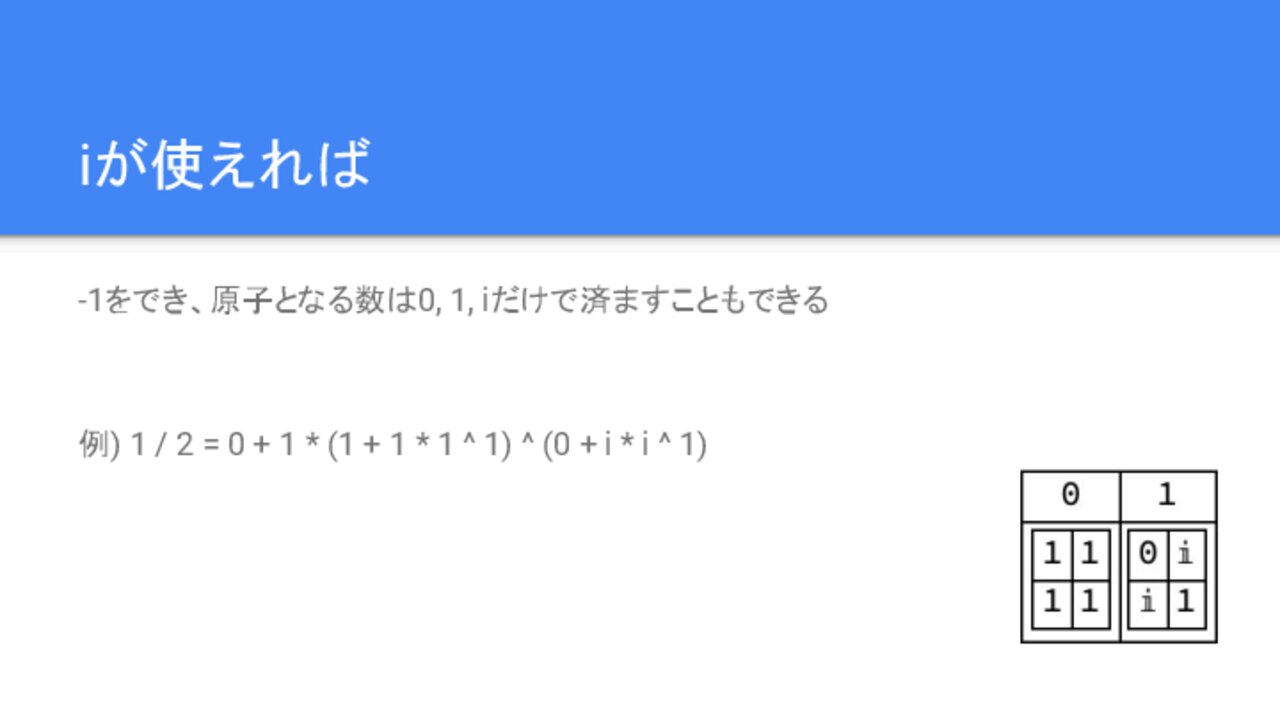
-1を作ることができ、原子となる数は0, 1, iだけで済ますこともできます。

例)

1 / 2 = 0 + 1 * (1 + 1 * 1 ^ 1) ^ (0 + i * i ^ 1)

eも使えれば

三角関数を定義できます（ついでにπも使えるとなおよし）

cos(x)  = (e^(- i x) + e^(i x)) / 2

なんでも入れられるわけじゃない

0 + 0 * 0 ^ 0 ⇒ 0^0を含んでいるので不定値

0 + 0 * 0 ^ i (虚数乗) ⇒ 0^iを含んでいるので不定値

0 + 0 * 0 ^ -1 (負数乗) ⇒ 0除算

このように、定義するのが難しい組み合わせは出てきてしまいます。

課題

数の別表現が排除できない（一意性がない）のが難点です。

もっと幅広く「関数」あるいは「特殊関数」を表せられるか（logとか）も気になります。

頻出の数をより小さい組み合わせで作れるもっといいブロックを定義できるか、新しいアイデアも浮かんできているので次回のプレゼンで発表するかもしれません。

まとめ

万能ブロックによって代数的数相当の任意の数を表現可能になりました。

定義した万能ブロックで4変数関数を2x2配列で可視化できます。

複雑な式はブロックも複雑になってしまうが、慣れれば読めそうなシンプルな構造です。

以上

ご静聴ありがとうございました。

総括

今回の日曜数学会の発表は、いつもより好評だった感触があります。

いつもブッコミ過ぎるので、あまりブッコミすぎないボリュームで、イメージしやすいのが成功ポイントだったかなと思います。

次回の日曜数学会は10月頃にありますので、ご興味のある方は日曜数学会のXアカウントをフォローのうえぜひご参加ください。