研究2024-08-20: 立方球面直交座標系

わたし的 理想の球面座標系

かれこれ社会人時代だったか、大学生時代だったか、高校生時代だったかも忘れてしまいましたが、とある球面座標系を着想していました。

というのも、緯度と経度を使ういわゆる「極座標系」に大いなる不満を持っていたのです。

緯度と経度をxyとして考えると、対称的ではない、と言えばおわかりでしょうか。

私が考えていたのは、単位球面上でグリッドを作ったときにx方向とy方向を入れ替えても対称な座標系です。

導出過程

イメージとしてはこんな感じです。

わたし的 理想の球面座標（第一形態） pic.twitter.com/kRyTIxbhdE

— 岩淵夕希物智 (@butchi_y) August 14, 2024

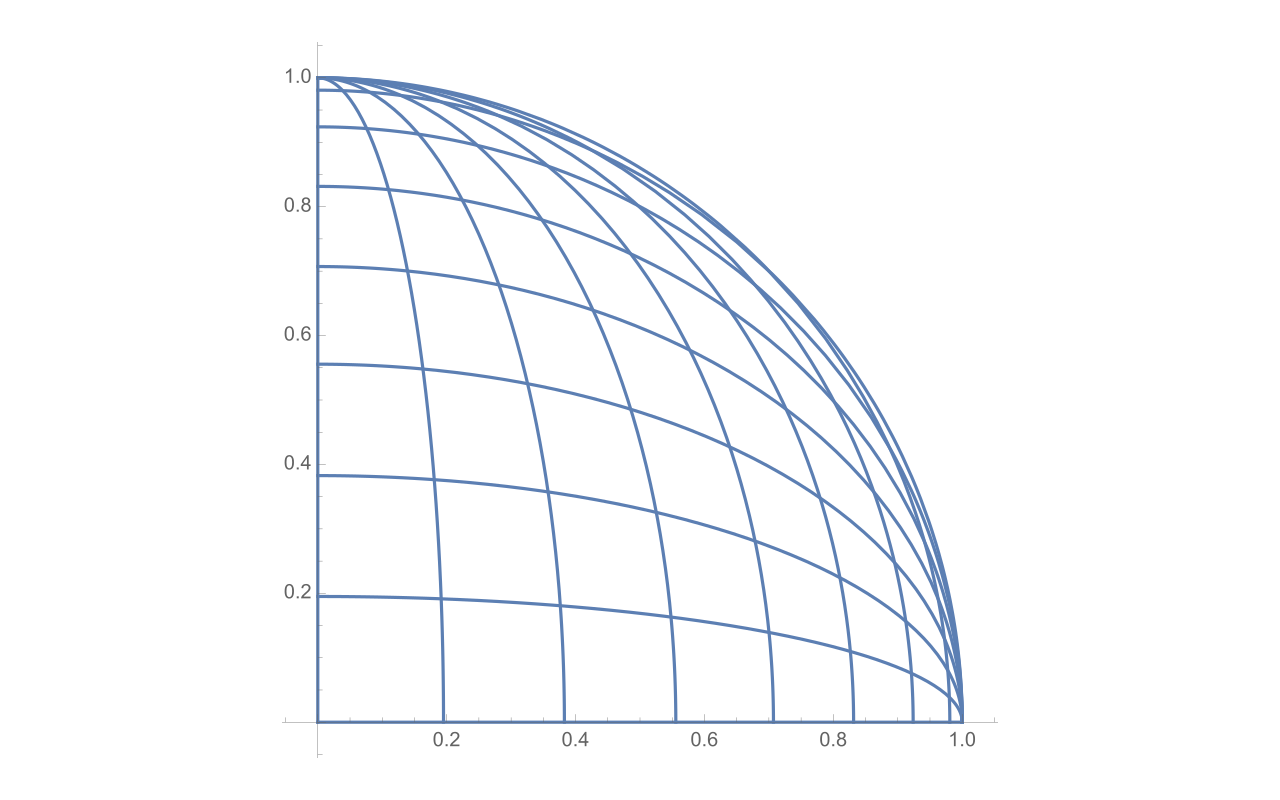
球面の中心近くが直交座標になっていて、上下左右に対称的です。

ただ、ここでは立式が完全ではありませんでした。

Graphics[{Table[
   Line[Table[{Cos[s] Cos[t], Sin[t]}, {t, -Pi, Pi, 1/256}]], {s, -Pi,
     Pi, Pi/16}], 
  Table[Line[
    Table[{Cos[t], Cos[s] Sin[t]}, {t, -Pi, Pi, 1/256}]], {s, -Pi, Pi,
     Pi/16}]}]

いちおう図形としては描けましたが、ここから格子点をうまく生成できませんでした。

とりあえずZ方向を無視してXY平面だけで考えてイメージを掴みました。

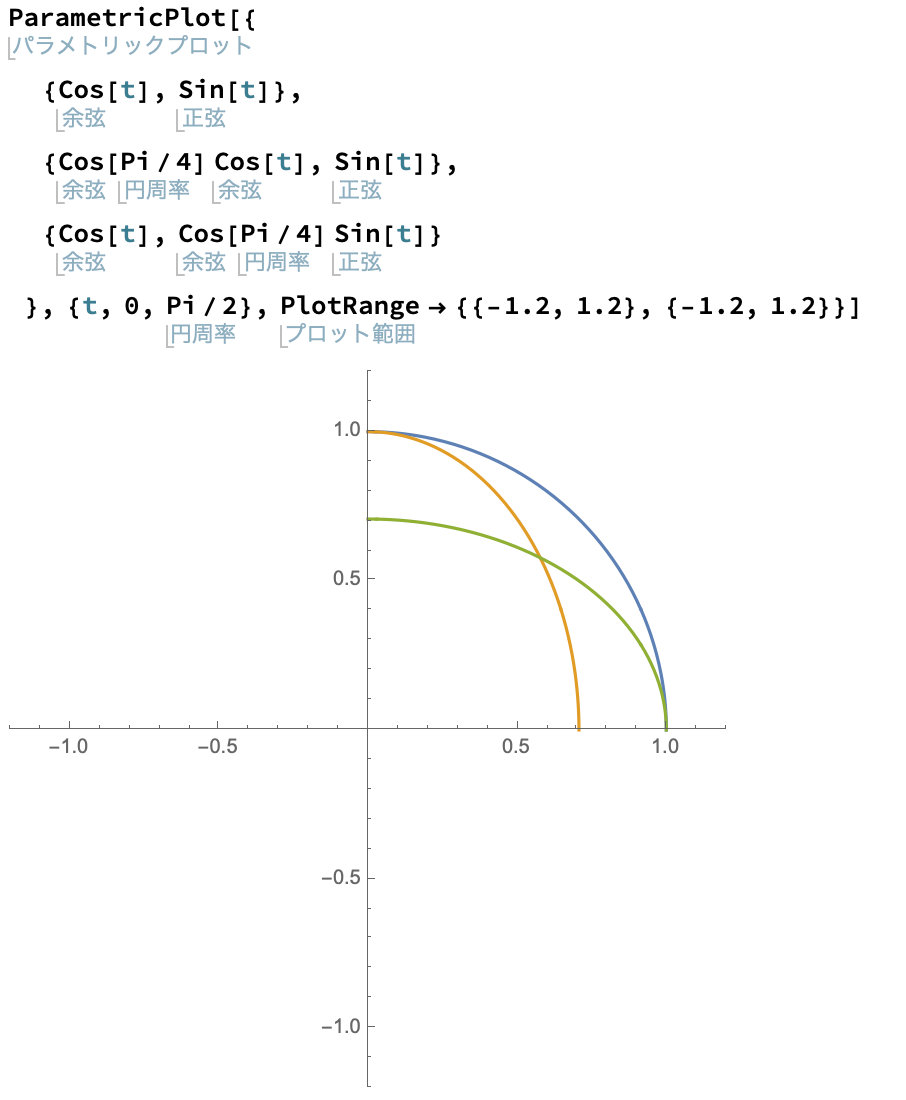
今思えば、ここの時点で深堀りしていればクリアだったのですが、紆余曲折をしてしまいました。

適当に立式するも噛み合わず。

ChatGPTでGPT-4oとWolframのGPTsを使ってみてなかなかいい線まで行ったのですが、核心までは触れられませんでした。

しかし、WolframのGPTsはWolframAlphaとの連携が上手くできている一方、素のChatGPTも単なる言葉遊びではなくPythonを実行して計算しているようで、今回は正解にたどり着かなかったものの問題によってはかなり使えそうです。

球面三角法

球面座標系における球面余弦定理、特に球面上のピタゴラスの定理は着想当初から目をつけていました。

また、球面三角法の正弦定理も新たに目をつけました。

ただ、紙と鉛筆（なんと今回はなぜか緑の色鉛筆を使って研究していました）を使って図に描いてもなかなか進まず泥沼化してしまいました。

解答

平面に投影したXY座標上では、 倍に縮小した縦長の楕円と 倍に縮小した横長の楕円の交点が座標になります。

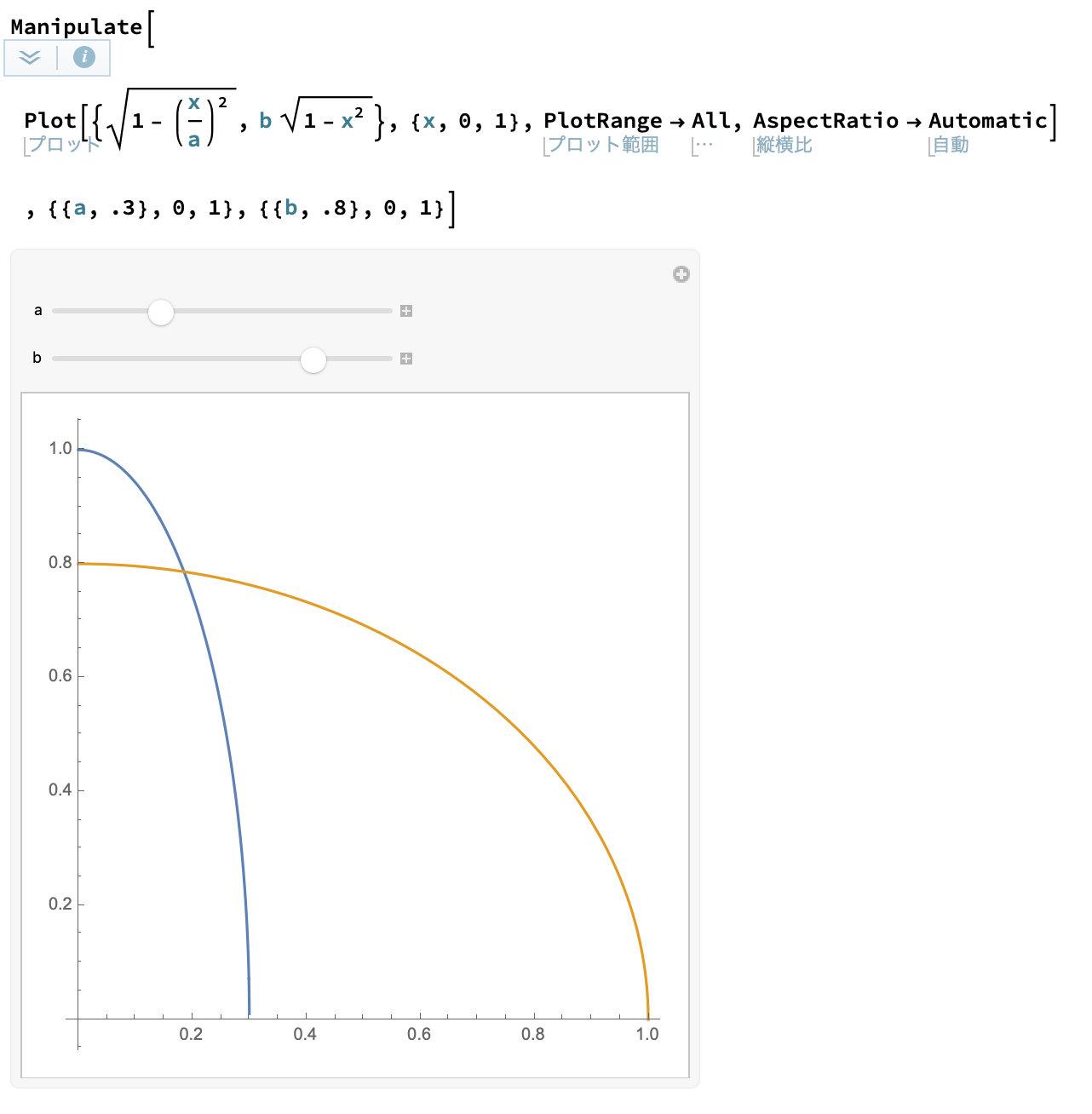
Solve[Sqrt[1 - (x/a)^2] == b Sqrt[1 - x^2], x]

ちょっと雑な式ですが、ようやく所望らしき格子点が得られました！

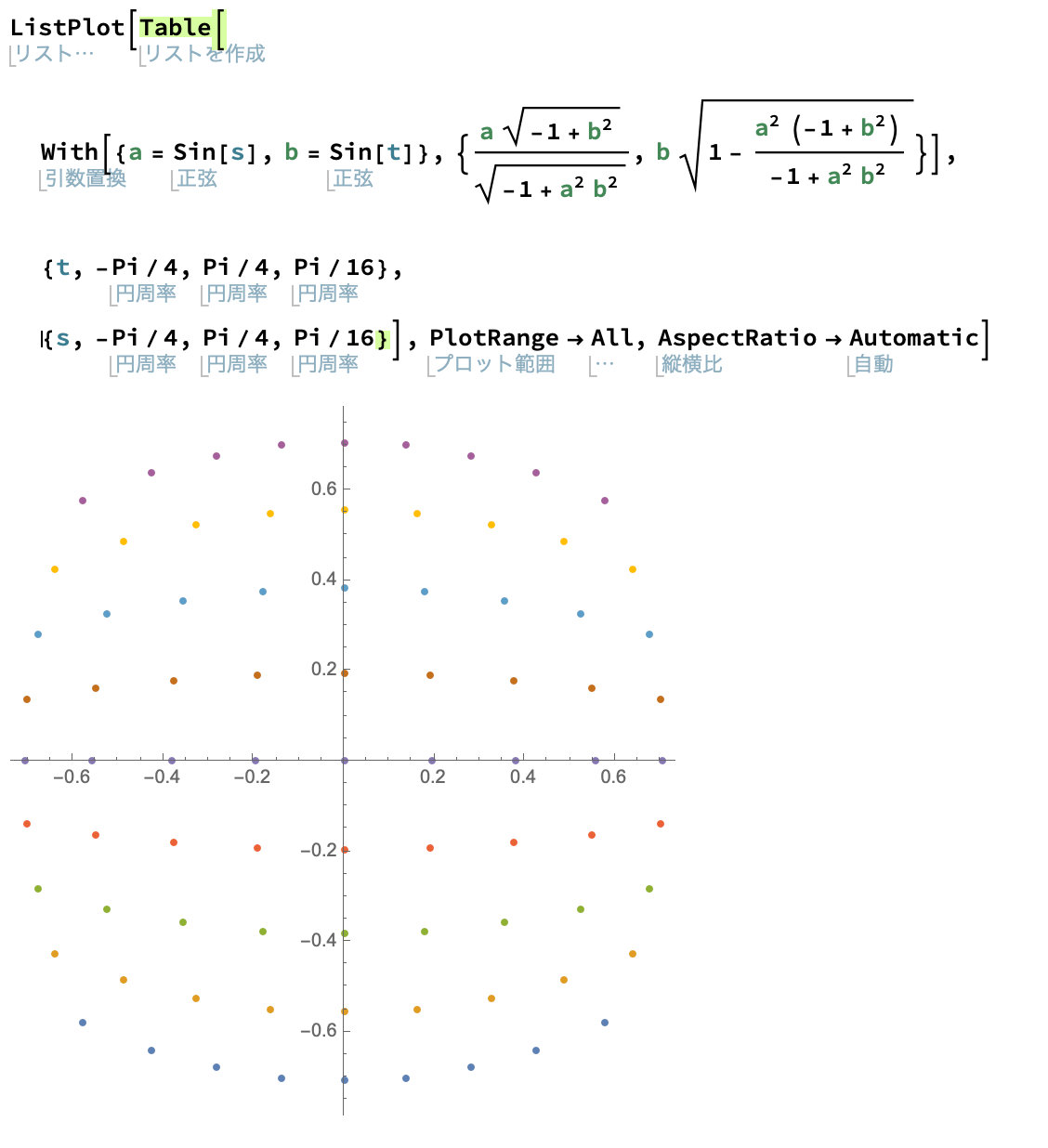
変数をsinに変換して

これはかなりすっきり！ （zは を式変形して導出）

これです！これが長年求めていた座標系！

これはプロット範囲を の代わりに としたものです。

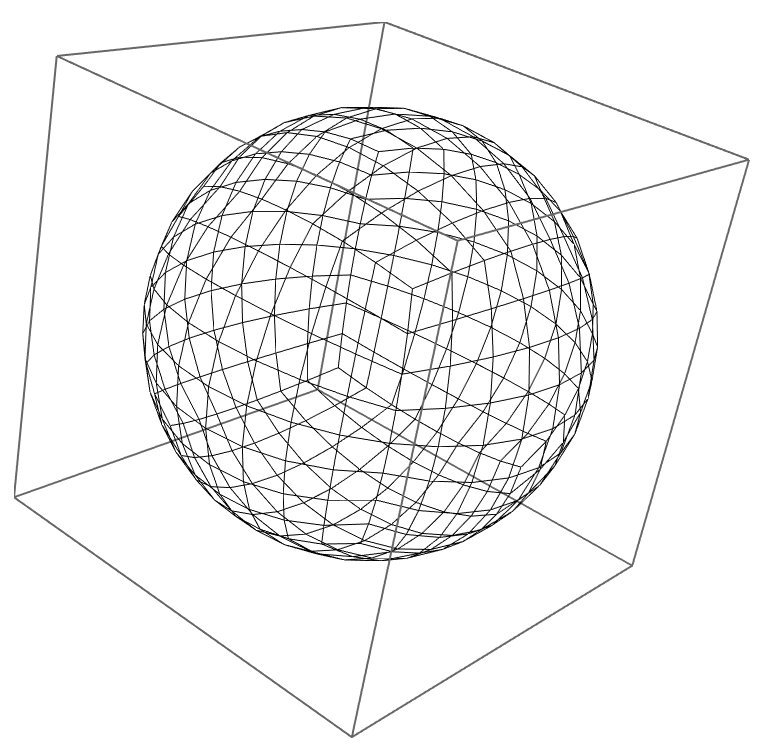
それをさらに立方体状に貼り合わせたらさらに安定した座標系になります。

ただ、結果が出てから画像検索をしてみたら、「カトマルクラーク」(Catmull-Clark再分割)という手法と非常に類似していました。

こちらの図形は、正八面体を基本としています。
そのため、3価の頂点が8つあります。

Catmull-Clark再分割というCGの分野でよく知られた分割方法を適用して作りました。 pic.twitter.com/gjV6GDgLmp

— 三谷 純 Jun MITANI (@jmitani) February 22, 2020

これ、分割自体は今回の数式に一致しているのでしょうかね？

車輪の再発明でなければ嬉しいけれど、長年の(自分にとっての)未解決問題が解けたのは感慨深いです。

苦しみもあったけれど楽しかった！