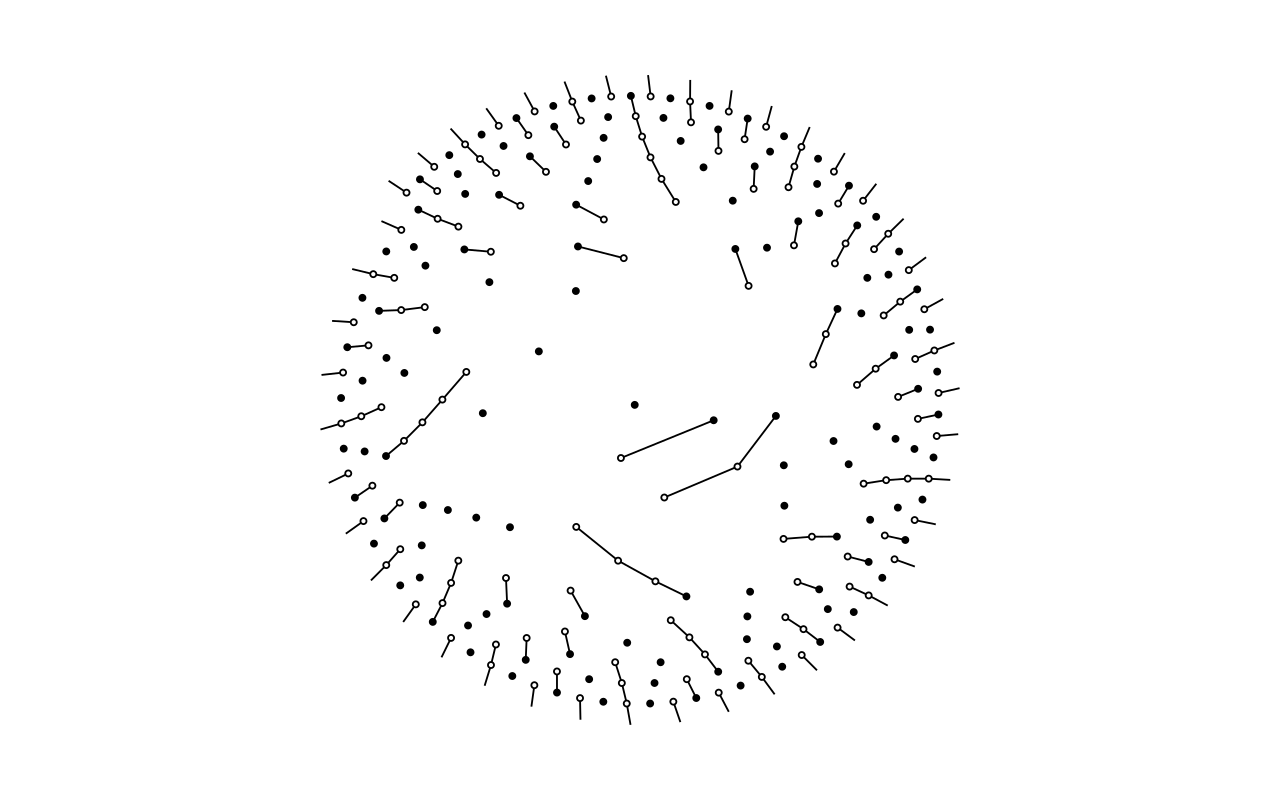
コラッツの最初の難関

コラッツの問題は定義はとても簡単、でも問題としてはかなりの難問で未解決、という稀有な問題です。

奇数なら3倍して1を足す、偶数なら2で割る、それだけの話。

たとえば3という数は奇数なので3倍して1を足したら10、10は偶数なので2で割って5、5は奇数なので3倍して1を足したら16、16は偶数なので2で割って8、そこから4→2→1と半分にして、そこからは1→4→2→1→4→2...とループになります。

十いくつぐらいでスタートするなら手計算で楽しく計算できますが、27はかなり手強いです。

で、27以降もさらなる強敵がいて、そんな強敵も計算し尽くしてどんな数でも1→4→2のループに落とし込める（1に到達する）という予想が コラッツ予想 です。

いま解ければ1億2000万円の懸賞金がもらえます！

本来の定義

このような関数（コラッツ写像）のネストがコラッツの遷移です。

先ほど手強いと言った27は以下のような遷移になります。

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 
242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 
700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 
668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 
638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 
7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 
4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 
122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 
16, 8, 4, 2, 1

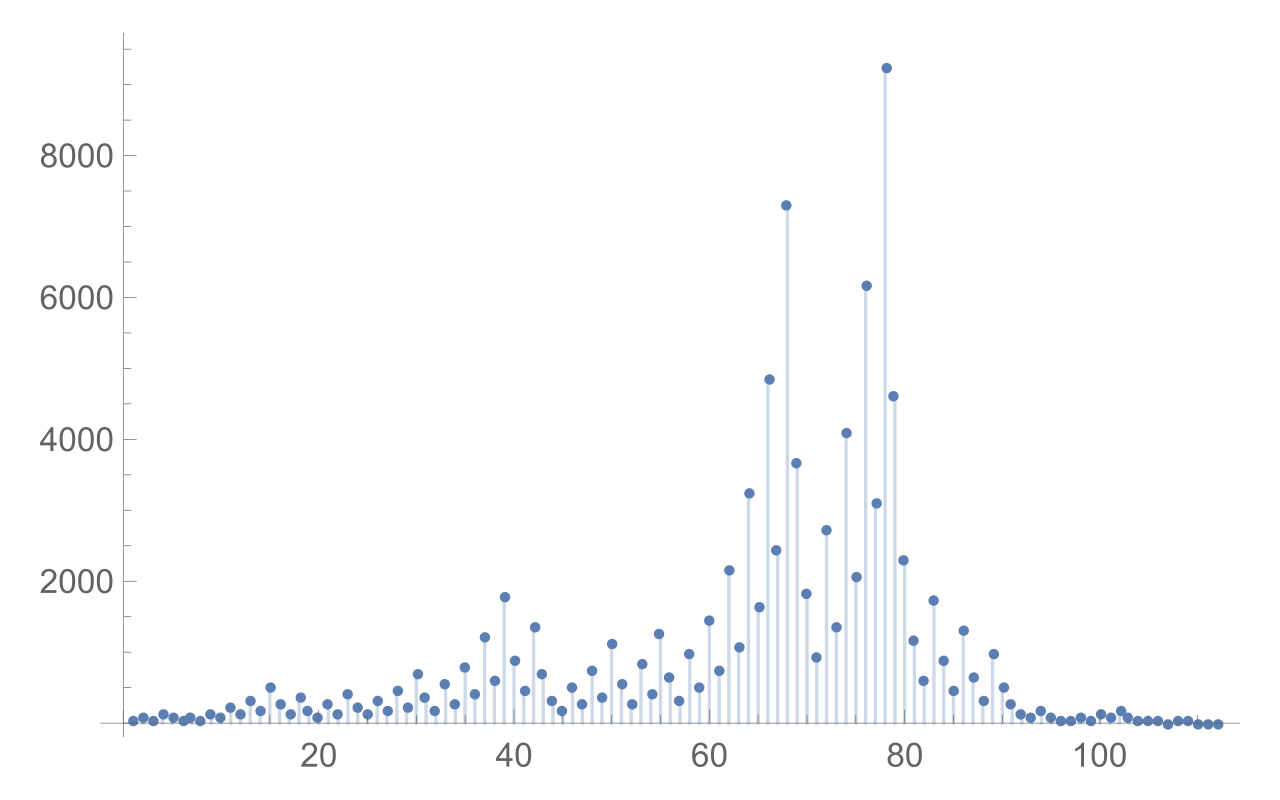
奇数から奇数への写像

コラッツ写像に偶数が与えられたときは何ステップか偶数のまま遷移が長く続くときがあり、これを冗長だと考えて省略する方法をとることがあります（といいつつ、文献ではあまり見かけないので個人的に嬉しいということで）。

本記事では以下の定義による写像を 奇数コラッツ写像と呼ぶことにします。

ちょっと複雑な定義かもしれませんが、要は「nが偶数のときは2で割る」を「nが偶数のときは(奇数になるまで)2で割れるだけ割る」と置き換えただけです。

結果としては偶数が省かれるので、27の遷移も以下のように簡略化されます。

27, 41, 31, 47, 71, 107, 161, 121, 91, 137, 103, 155, 233, 175, 263,
395, 593, 445, 167, 251, 377, 283, 425, 319, 479, 719, 1079, 1619,
2429, 911, 1367, 2051, 3077, 577, 433, 325, 61, 23, 35, 53, 5, 1

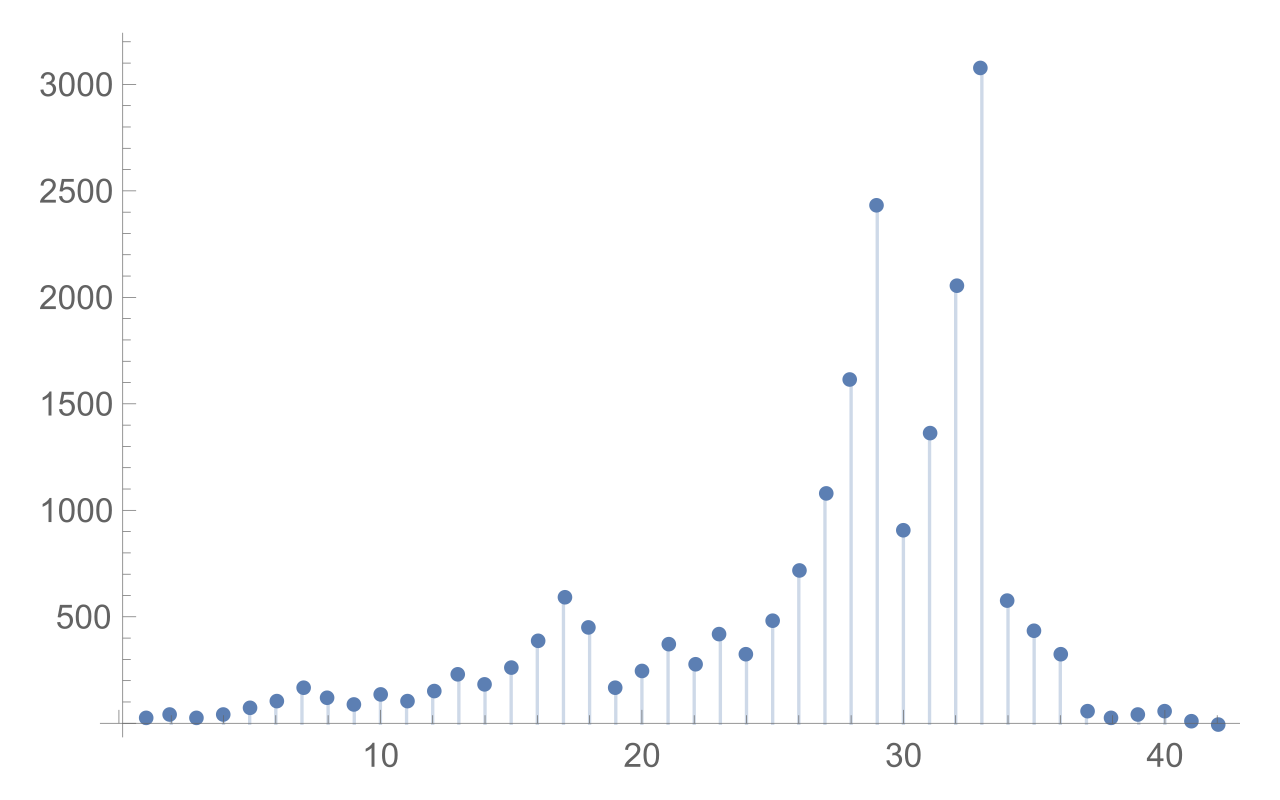
1に到達したら1→1の無限ループになり、そこは無視します。

後述の図から分かったことですが、奇数から奇数の遷移は以下の式とおそらく同値です。

コラッツの整数螺旋

突然ですが、奇数コラッツ写像をうまく平面上にプロットできた、というのが今回のメインの報告です。

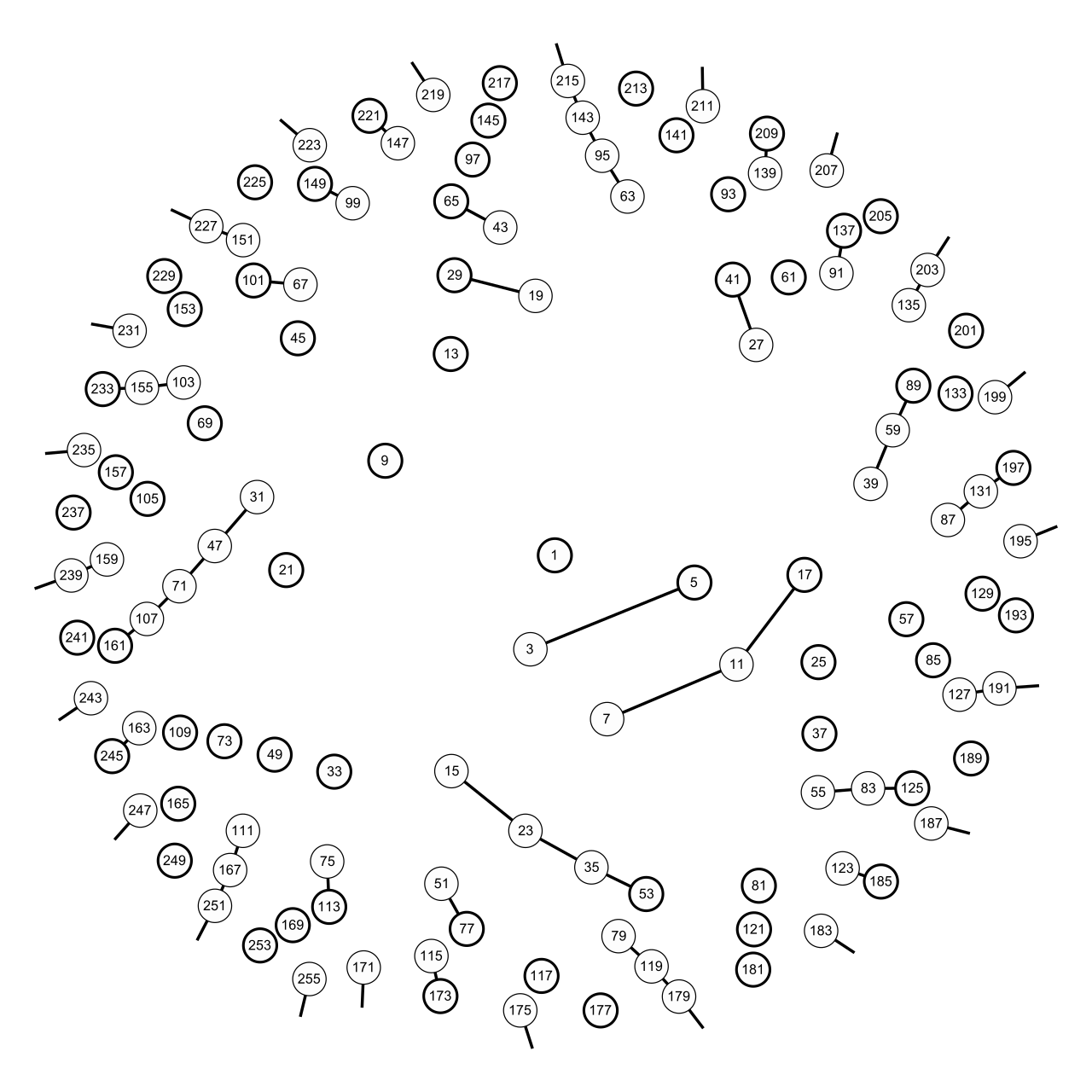
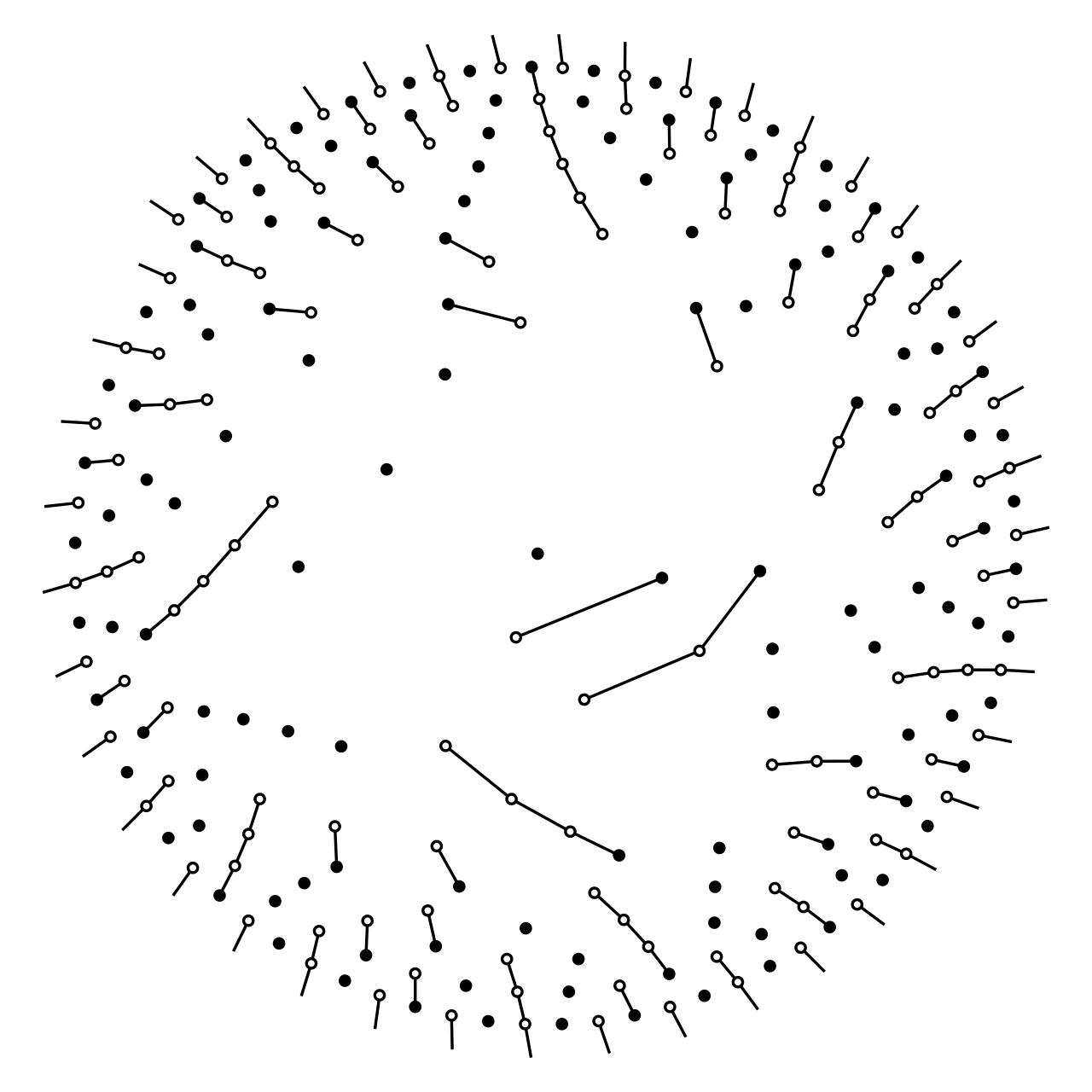
この形式のプロットは改めてブログ記事にしようと思いますが、放射と螺旋によってできる整数の螺旋、「整数螺旋」と今のところ名付けています。そして今回プロットしたのが「コラッツの整数螺旋」です。

奇数から奇数への遷移が続いて最初のピーク値（局所的最大値）になるまでの数の遷移を線でつないであります。たとえば、31からスタートすると 31→47→71→107→161→121→91→137→103→155→...53→5→1と遷移しますが、最初のピーク値が161なので31→47→71→107→161の5ステップが経路長となります。

なお、 型の奇数は3倍して1を足すと と2で割れるようになり 型の奇数は3倍して1を足すと と4で割れるようになります。

つまり、 型の奇数は約 倍に増え、 型の奇数は約 倍に減る、ということを示しています。

この奇数初期値からピーク奇数への遷移、なんだか規則性のありそうな経路長を持っています。

先ほどの「2で割れるだけ割る」と同様の操作で、「2で割れる回数」を表す関数となります。

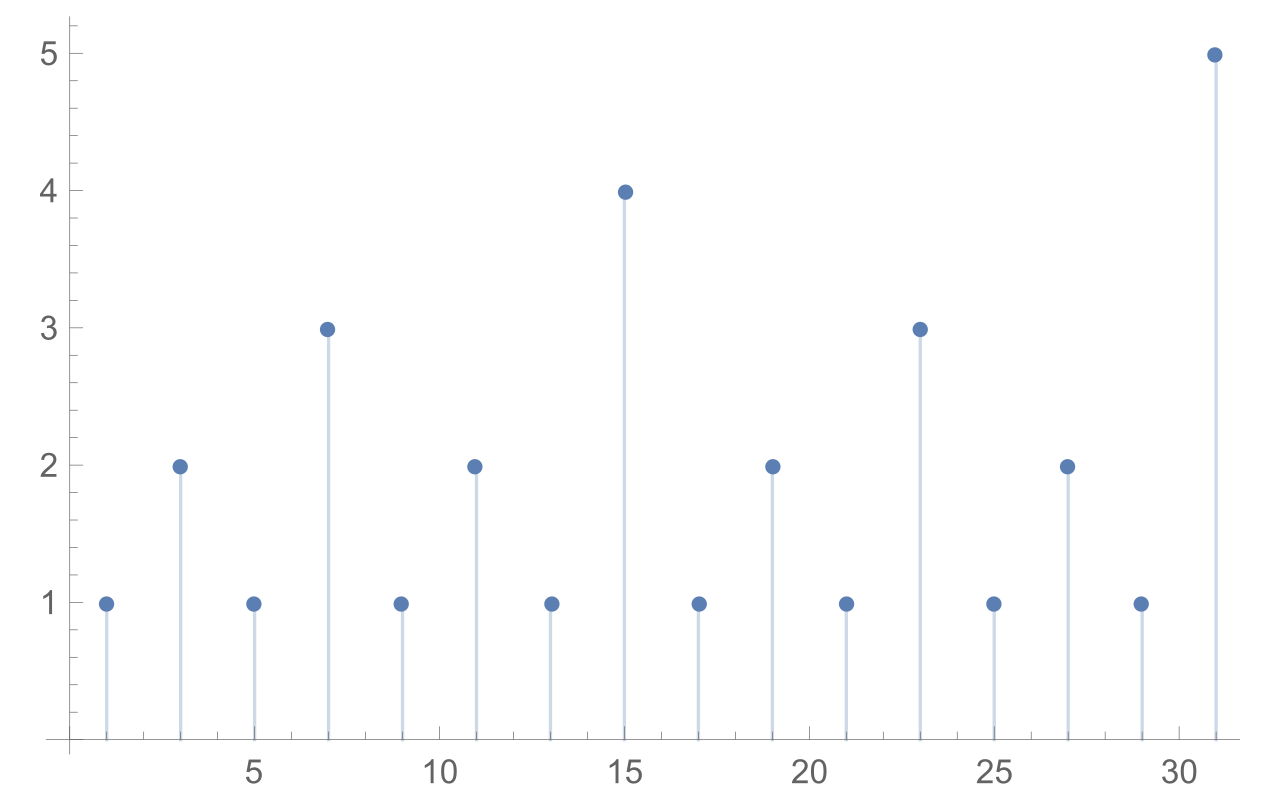
このことから、初期値の奇数から最初のピーク値までの奇数遷移ステップ数は、倍増しても高々1ステップずつしか増えないということを示しています。

どこまでわかったか

コラッツ写像に奇数の初期値を与えると、約 倍の奇数への増加を規則性のある一定ステップ繰り返します。

型の奇数に到達してから一旦 の減少をするところまでの奇数の挙動が完全に解明できたわけですが、27から始まる長い遷移もじつは最初の27→41しか見えてないので、そこから起死回生の増加（ラッキーな遷移）を何回も繰り返して無限増殖するような挙動をすることはまだ否定できていません（たぶん）。

また、増加する経路は見えたものの、同じく減少してからのパスに終端の1→1以外のループが存在しないことも否定できていません（たぶん）。

まとめ

冒頭でも述べた通り、コラッツの問題はとても簡単に理解できるようで、とても難しい問題です。

定義が簡単なだけに、「コラッツの問題解けた！」と豪語する人が後を絶ちませんが、危うく私も今回の発見で「コラッツの問題解けた！」と言い切りたくなってしまいそうでした。

ただ、今回紹介した奇数から奇数への遷移はコラッツの問題をかなり見通せる方法で、整数螺旋による可視化は私としてはかなり大きなアドバンテージでした。

やっぱり言語化・明文化は大事ですね。

皆さんも、コラッツの問題をさまざまな視点で見てみると新しい発見があるかもしれません。

ただし、くれぐれもコラッツ予想の解決で人生を棒に振らないようにご注意を。