トゥエ・モース列で描くコッホ曲線
トゥエ・モース列で描くコッホ曲線
トゥエ・モース列という列は
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, ...
という 01 列です。この数列の法則、見つけられますか？
トゥエ・モース列の作り方
トゥエ・モース列 (Thue-Morse) を作るひとつの方法は、以下の文字列の増やし方で長い文字列を得ることです。
前回ご紹介したフィボナッチ文字列では、二項漸化式として直前の 2 つの項が基本的には必要でしたが、これは 1 つ前の項だけで次の項が求まります。
そして、これを 01 列として並べた
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, ... (0110100110010110...)
をトゥエ・モース列 (Thue-Morse sequence)と言います（表記揺れで「スー・モース列」とされている文献もあります）。
こんなコッホ曲線の描き方があった
という数列を、日曜数学会や数学デーのキグロさんが最近自力で発見したようで、それを改めて調べていたのが今回の記事執筆のきっかけです。
同じパターンが3連続することが決してない数列（のはず）。
— キグロ＠カクヨム (@kiguro_masanao) May 18, 2024
0が3連続することも、1が3連続することも、01が3連続することも、10が3連続することも、001や010や011や100や101や110が3連続することも決してない（はず）。 pic.twitter.com/WU13jln1uw
それで、トゥエ・モース列はWolfram 言語の ThueMorse 関数のページにもあったよなと調べていたら、アプリケーションの項で、なんとトゥエ・モース列を元にコッホ曲線が描けるとのことです。
Graphics[Line[AnglePath[Array[ThueMorse, 4096] 2 Pi/3]]]
あまりにもさらっと書かれているので拍子抜けしましたが、トゥエ・モース列にしたがって 60 度ごと角度を変えたタートルグラフィックスで描いているようです。
ただ、ページに書かれていたのは 4096 サンプルでの描画で、以下のように 256 サンプル、1024 サンプルと変えてみて、かなりごまかしたようなパスになっていました。
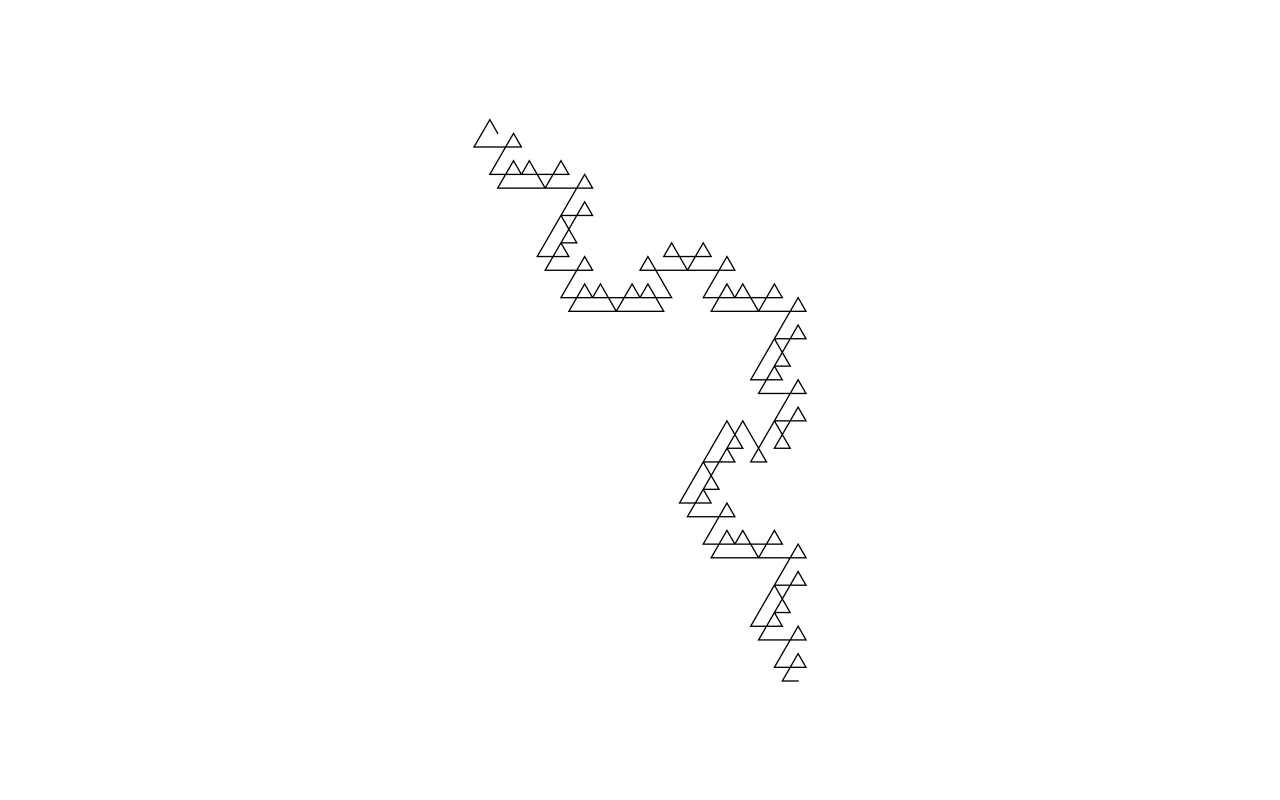
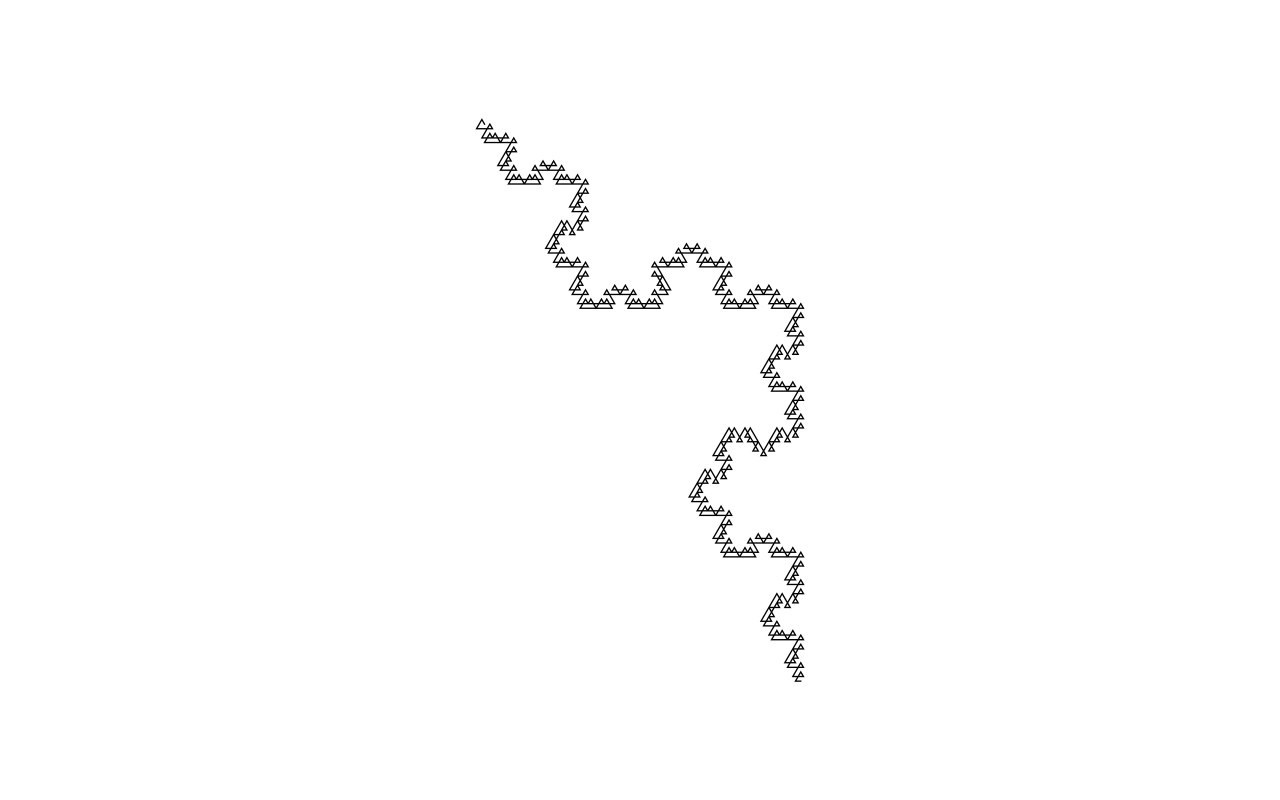
しかしながら、一見つながりがないようなところでフラクタルが出てきたりするのは面白いですね。
それではまた。