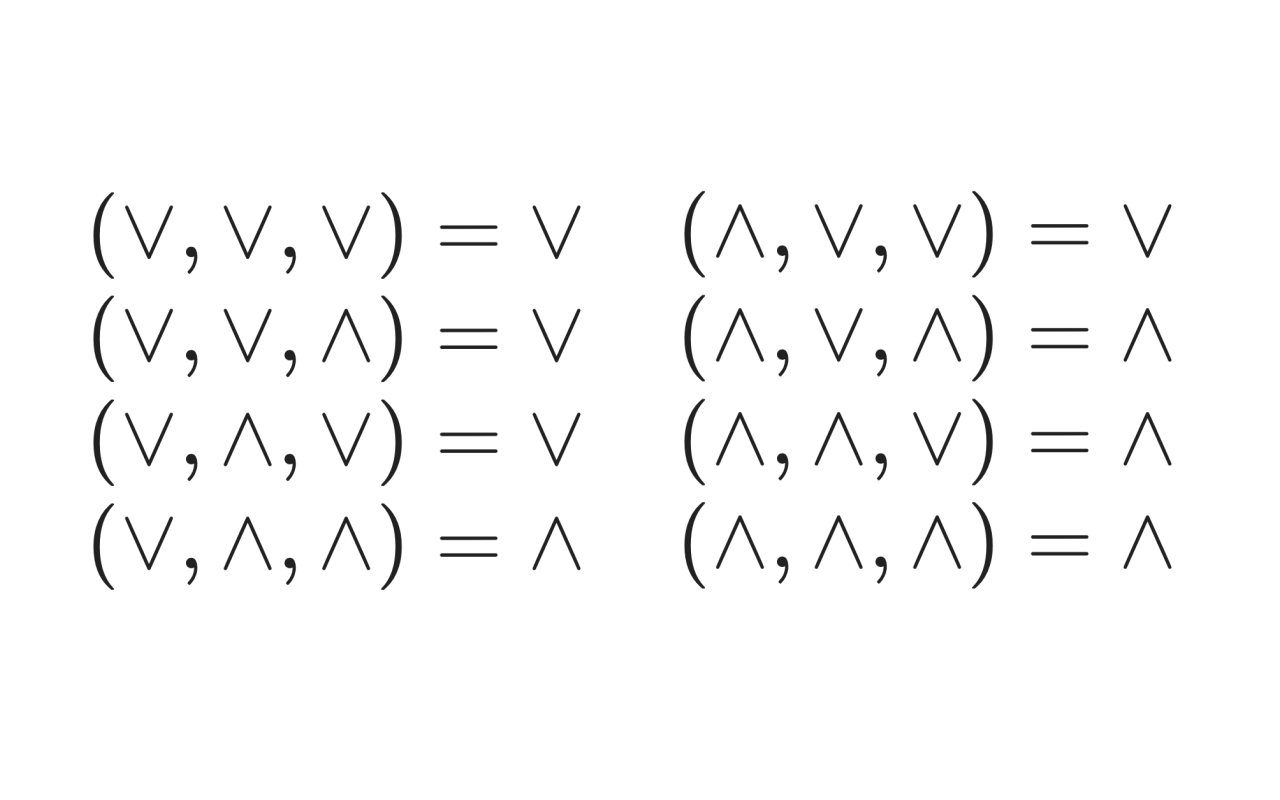演算を引数として持つ関数
演算を引数として持つ関数
（※ 記号の扱いに関する話として、頭がこんがらがるような話題ですので、注意して読み進めてください。）
ちょうど昨日の記事で、「演算同士の演算」について考えました。今日はその続き、「演算を引数として持つ関数」になります。
昨日の記事で取り上げた、一見暗号のような次のような表記を思い出してください（並びは変えています）。
これは、本来は「演算同士の演算」として考えるべきものですが、これって単に眺めると記号が列として3つ並んでいるだけなので、適当に関数 でラップしたものとして「演算を引数として持つ三変数関数」として捉え直すこともできるのでは、と。
つまり、
と書き下せます。
別にラップせずに、「列がなんらかの値を示す」とだけ考えてもいいです。
（なお、前回の記事では中置演算子を使っていましたが、今回は全て前置演算子に統一していますのでご注意ください。）
演算結果は恣意的だったりもしますが、あくまでもクイズとして、上の関数（対応づけ）はどのような法則を持っているか少し考えてみてください。
正解は…
多数決論理
「多数決」！
つまり、引数に与えられた3つの論理演算のうち、多数を占めるものがそのまま結果になる、というものです。
例えば、 の場合、引数に が2つ、 が1つあるので、多数を占める が結果になります。
一般に、ブール値の論理演算として、多数決論理などと呼ばれています。
列と関数の関係（Wolfram言語の場合）
関数と引数の組を、ひとまとめにしてひとつの列として捉える、というのは数学的にはあまり馴染みがないかもしれませんが、プログラミング言語、とりわけ記号処理に強いWolfram言語（Mathematica）などでは、関数と引数の組をそのまま列とみなして扱うことができます。
実際、次のような表現で関数に演算を引数として与えたとします。
s = a[b, c, d]
b, c, dをaに適用する、という意味合いのように見えますが、これはあくまでも見栄え上の話であり、実際には a、b、c、d は記号でしかなく、じつは、 [a, b, c, d] という配列的ななものを表しているに過ぎません。
例えば、次のようにして「0番目」から「3番目」までの要素を取り出すことができます。
s[[0]] (* => a *)
s[[1]] (* => b *)
s[[2]] (* => c *)
s[[3]] (* => d *)
このように、関数の役割を持っていそうな記号も、（Headという特別な役割を持っているものの）配列のように振る舞う、というのがWolfram言語の面白いところです。
ちなみに、前回の記事からの検証もWolfram言語で行っており、記号の処理としての強みが生きていてとても計算が楽でした。
記号の処理、ということで、もしかしたら変な挙動になる場合もあったかもしれませんが、形式的には
1[2, 3]
のように、数値をHeadとして扱うこともできるにはできます（少なくともこの式の評価時にはエラーとはなりません）。
もっと簡単な例
もっと簡単な例として、2つの演算子の引数を持つ関数を考えます。
gという関数を適用する、というのを言い換えると、「第一引数として与えられる関数に第二引数として与えられる引数を適用する」ということになります。
つまり、
となります。
今回は、 と は、扱いとしては「単項マイナス演算子」（符号反転）のような、一つだけの項に対して作用するものとして考えます。
4通りの計算に対して2値の結果を与えるような関数を考えると、 通りの関数が考えられるのですが、ブール演算ともなれば、何らかの意味づけを与えられたりもします。
例えば、次のように定義してみます。
この場合、 は次のような真理値表で表せます。
| 引数1 | 引数2 | |
|---|---|---|
真理値表を元にしてgの振る舞いを考えると、 は「第一引数が のときに を返し、 のときに を返す」というものになります（引数2は無視されている）。
一方で、 引数1の関数としての振る舞いは、 は「常に を返す関数」、 は「常に を返す関数」として捉えられます。
もうひとつの例として、
の場合、次のような真理値表になります。
| 引数1 | 引数2 | |
|---|---|---|
この場合、 は「引数1と引数2が同じときにその値を返し、異なるときにもう一方の値を返す」というものになります。ブール演算としては、XOR（排他的論理和）に相当します。
一方で、引数1の関数としての振る舞いは、 は「引数2をそのまま返す関数」 (Identity)、 は「引数2を反転して返す関数」 (NOT) として捉えられます。
おわりに
前回の記事から引き続き、演算を元として持つ集合を考えるのはなかなか面白いです。
演算と要素を混在させた集合を考えると、より複雑な構造でも柔軟に捉えられそうで、今後の研究のヒントになりそうです。
（ただ、やっぱり記号が演算なんだか文字列なんだか要素なんだか混乱しそうで危ういですが…。）
